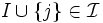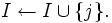マトロイド
【英】:matroid
概要
マトロイドとは, ベクトル集合の一次独立性・従属性といった概念を組合せ論的に抽象化することによって得られる公理系を満たすものである. 1935年にホイットニー(H. Whitney)が導入し,1950年代以降タット(W. T. Tutte)らにより研究が発展してきた. 1960年代にエドモンズ(J. Edmonds)によって数理計画法における重要性が指摘されて以来, マトロイドは, 効率的に解くことのできる離散最適化問題を把握する枠組として中心的な役割を担っている.
詳説
マトロイド (matroid) は, 線型空間内のベクトル集合の一次独立・従属といった概念の組合せ論的な側面を抽象化して得られる公理系を満たすものとして定義されている. 有限集合  とその部分集合族
とその部分集合族 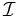 が以下の (I0)-(I2) を満たすとき,
が以下の (I0)-(I2) を満たすとき,  はマトロイドと呼ばれる.
はマトロイドと呼ばれる.
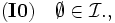
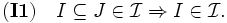
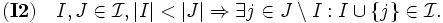
マトロイド 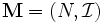 において,
において,  を
を 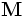 の台集合,
の台集合, 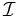 を独立集合族 (independent set family) という.部分集合
を独立集合族 (independent set family) という.部分集合 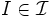 は,
は, 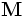 の独立集合と呼ばれる.
の独立集合と呼ばれる.
マトロイド 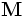 の基とは, 極大な独立集合のことである. 公理 (I2) から明らかなように, 基の要素数は全て等しい. この数をマトロイド
の基とは, 極大な独立集合のことである. 公理 (I2) から明らかなように, 基の要素数は全て等しい. この数をマトロイド 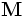 の階数という. 基の全体を
の階数という. 基の全体を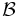 と書き,
と書き, 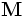 の基族 (base family) と呼ぶ. 基族
の基族 (base family) と呼ぶ. 基族 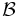 は以下の (B0)-(B1) を満たす.
は以下の (B0)-(B1) を満たす.
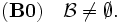
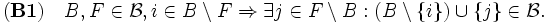
マトロイド 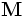 の階数関数 (rank function)
の階数関数 (rank function) 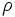 は,
は,
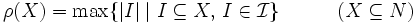
と定義される. 階数関数 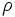 は以下の (R0)-(R3) を満たしている.
は以下の (R0)-(R3) を満たしている.
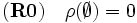 .
.
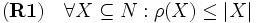 .
.
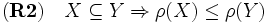 .
.
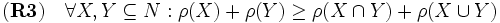 .
.
特に, (R3) は 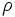 が劣モジュラ関数 (submodular function) であることを示している.
が劣モジュラ関数 (submodular function) であることを示している.
ここでは, (I0)-(I2) によってマトロイドを定義したが, (B0)-(B1) を満たす基族 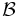 からマトロイドを定義することもできる. この場合, 独立集合は基の部分集合として定義される. 同様に, (R0)-(R3) を満たす階数関数によってマトロイドを定義することもできる. この場合, 独立集合族は
からマトロイドを定義することもできる. この場合, 独立集合は基の部分集合として定義される. 同様に, (R0)-(R3) を満たす階数関数によってマトロイドを定義することもできる. この場合, 独立集合族は 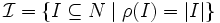 によって定められる.
によって定められる.
グラフ的マトロイド (graphic matroid) 点集合  , 枝集合
, 枝集合 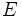 を持つ無向グラフ
を持つ無向グラフ 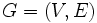 を考える. 枝集合の部分集合のうち, 閉路を含まないものの全体を
を考える. 枝集合の部分集合のうち, 閉路を含まないものの全体を 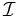 とすると,
とすると, 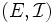 は (I0)-(I2) を満たし, マトロイドになる. このようにして得られるマトロイドをグラフ的マトロイドと呼ぶ.
は (I0)-(I2) を満たし, マトロイドになる. このようにして得られるマトロイドをグラフ的マトロイドと呼ぶ.
横断マトロイド (transversal matroid) 点集合 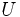 ,
,  , 枝集合
, 枝集合 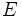 からなる2部グラフ
からなる2部グラフ 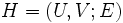 を考える. 枝部分集合
を考える. 枝部分集合 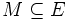 で端点を共有しないものを
で端点を共有しないものを 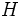 のマッチングという. 点集合
のマッチングという. 点集合 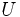 の部分集合で,
の部分集合で, 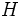 のマッチングの
のマッチングの 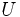 における端点集合となり得るものの全体を
における端点集合となり得るものの全体を 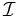 とする. このとき,
とする. このとき,  は (I0)-(I2) を満たし, マトロイドになる. このようにして得られるマトロイド
は (I0)-(I2) を満たし, マトロイドになる. このようにして得られるマトロイド  を横断マトロイドと呼ぶ.
を横断マトロイドと呼ぶ.
マトロイド 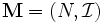 の各要素
の各要素 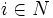 に重み
に重み 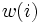 が与えられたとき, 以下の様な貪欲アルゴリズム (greedy algorithm) を適用して最終的に得られる
が与えられたとき, 以下の様な貪欲アルゴリズム (greedy algorithm) を適用して最終的に得られる 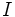 が, 重み最小の基, すなわち,
が, 重み最小の基, すなわち,  を最小にする基
を最小にする基 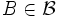 となる.
となる.
全く同様のアルゴリズムによって, 重み最大の基を求めることもできる.
離散最適化におけるマトロイドの重要性は, 貪欲アルゴリズムのみならず, 共通マトロイド問題 (matroid intersection problem) に負うところが大きい. 共通マトロイド問題とは, 台集合を共有するマトロイド 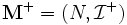 と
と 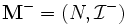 における共通独立集合のうちで, 要素数最大のものを求める問題である. この問題の最適値は,
における共通独立集合のうちで, 要素数最大のものを求める問題である. この問題の最適値は, 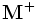 の階数関数
の階数関数 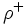 と
と 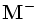 の階数関数
の階数関数 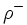 を用いて,
を用いて,
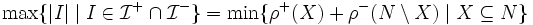
と特徴付けられる [1] . 共通マトロイド問題は, 回路理論やシステム解析においても本質的な役割を果たしている [2, 3, 5] .
マトロイドが, 行列における一次独立性を抽象化して得られたのに対し, 対称行列や歪対称行列の正則主小行列の組合せ的な性質を抽象化した概念として,デルタマトロイド (delta-matroid) が提案された. デルタマトロイドは, マトロイドの一般化であり, 貪欲アルゴリズムが適用可能であると同時に, 一般グラフ上のマッチングの端点集合族をも包含する枠組として注目されている.
また, 多項式行列の小行列式の次数の抽象化として付値マトロイド (valuated matroid) が提案された. 付値マトロイドの研究は, 劣モジュラ関数の凸性に関する理論と結び付いて, 離散凸解析と呼ばれる分野に発展している.
[1] J. Edmonds, "Submodular functions, matroids, and certain polyhedra," in Combinatorial Structures and Their Applications, R. Guy, H. Hanani, N. Sauer, and J. Schönheim, eds., Gordon and Breach, 69-87, 1970.
[2] 室田一雄, 「マトロイドとシステム解析」, 藤重悟 編『離散構造とアルゴリズムⅠ』, 近代科学社, 第2章,57-109, 1992.
[3] K. Murota, Matrices and Matroids for Systems Analysis, Springer-Verlag, 2000.
[4] J. G. Oxley, Matroid Theory, Oxford University Press, 1992.
[5] A. Recski, Matroid Theory and Its Applications in Electric Network Theory and in Statics, Springer-Verlag, 1989.
[6] D. J. A. Welsh, Matroid Theory, Academic Press, 1976.
[7] N.White (ed.) , Matroid Applications, Cambridge University Press, 1992.
[8] 伊理正夫, 藤重悟, 大山達雄,『グラフ・ネットワーク・マトロイド』, 産業図書, 1986.
[9] J. Lee, A First Course in Combinatorial Optimization, Cambridge University Press, 2004.
| グラフ・ネットワーク: | ポリマトロイド マッチング マッチング問題 マトロイド ユークリッド巡回セールスマン問題 付値マトロイド 共通マトロイド問題 |
- まとろいどのページへのリンク
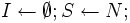
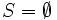 となるまで, 以下を
となるまで, 以下を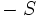 の中で,
の中で,  とする;
とする; 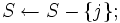
 もし
もし