一元配置分散分析

統計学用語辞典

一元配置分散分析

例題：
　「12 匹のラットに 3 種類の餌を与えたときの肝臓の重量は表 1 のようであった。餌の種類により肝臓の重量の母平均値に差があるといえいるか，有意水準 5% で検定しなさい。」

表 1．餌の種類による肝臓の重量

A餌	3.42	3.84	3.96	3.76
B餌	3.17	3.63	3.47	3.44	3.39
C餌	3.64	3.72	3.91

aov 関数を用いる場合 > d <- data.frame(x=x, g=as.factor(g)) # データフレームにする > summary(aov(x ~ g, d)) Df Sum Sq Mean Sq F value Pr(>F) g 2 0.31786 0.15893 4.6146 0.04175 * Residuals 9 0.30997 0.03444 --- Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 R による解析:

> x <- c(3.42, 3.84, 3.96, 3.76, 3.17, 3.63, 3.47, 3.44, 3.39, 3.64, 3.72, 3.91)
> g <- c(1,1,1,1,2,2,2,2,2,3,3,3)

oneway.test 関数を用いる場合

> oneway.test(x ~ g, var=T)

	One-way analysis of means

data:  x and g 
F = 4.6146, num df = 2, denom df = 9, p-value = 0.04175

> oneway.test(x ~ g)  # 等分散を仮定しないとき（Welch の方法の拡張）

	One-way analysis of means (not assuming equal variances)

data:  x and g 
F = 5.0045, num df = 2.000, denom df = 5.389, p-value = 0.05908

等分散でないときの平均値の差の検定によれば，「等分散を仮定しない検定法（Welch の方法の拡張）」を採用するのが良さそうである。

一元配置分散分析

　二次データに基づいて，一元配置分散分析を行う


例題：
　「4 つの群におけるある変数の測定値の集計結果は表 2 のようであった。母平均値に差があるといえいるか，有意水準 5% で検定しなさい。」

表 2．架空データ例

	件数	平均値	標準偏差
第1群	8	135.83	19.59
第2群	11	160.49	12.28
第3群	22	178.35	15.01
第4群	6	188.06	9.81
全体	47	168.17	22.40

R による解析:

> n <- c(8, 11, 22, 6)
> m <- c(135.83, 160.49, 178.35, 188.06)
> SD <- c(19.59, 12.28, 15.01, 9.81)
> my.oneway.anova(n, m, SD^2)	# この関数の定義を見る
$anova.table
                     SS d.f.        MS
between class 13669.396    3 4556.4655
within class   9406.843   43  218.7638
total         23076.240   46  501.6574

$result
           F        d.f.1        d.f.2            P 
2.082824e+01 3.000000e+00 4.300000e+01 1.737484e-08 

一元配置分散分析

　一元配置分散分析は，各群の分散が等しいことを前提にしている。分散の均一性をまえもって検定しておく方がよい。
　等分散でないときの平均値の差の検定によれば，「等分散を仮定しない検定法（Welch の方法の拡張）」を採用するのが良さそうである。
　等分散性を確かめてから一元配置分散分析という手順は，検定の多重性という点でも問題がある。最初から等分散を仮定しない一元配置分散分析を行う方がよい。


例題：
　「12 匹のラットに 3 種類の餌を与えたときの肝臓の重量は表 1 のようであった。餌の種類により肝臓の重量の母平均値に差があるといえいるか，有意水準 5% で検定しなさい。」

表 1．餌の種類による肝臓の重量

A餌	3.42	3.84	3.96	3.76
B餌	3.17	3.63	3.47	3.44	3.39
C餌	3.64	3.72	3.91

検定手順:

1. 前提
   • 帰無仮説 H0：「各群の母平均値は等しい」。
   • 対立仮説 H1：「各群の母平均値は等しくない」。
   • 有意水準 α で両側検定を行う（片側検定は定義できない）。
     　注：意味的に両側検定である。F 分布の片側確率を使うという形式的な意味では片側検定である。
   
   
2. 群の数を k，全ケース数を n，各群のケース数を nj，全体の平均値を ，第 j 群における平均値を 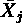とする（j=1， 2， ... ， k；Σ nj = n）。
   
3. 平方和 St を求める（全体の不偏分散 Ut が求められていれば，St = ( n - 1 ) Ut としてもよい）。
   
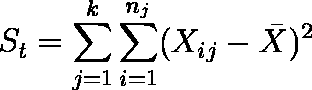
   例題の場合は，St = 0.6278 である。
   
4. 平方和 Sb を求める。
   
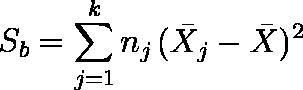
   例題の場合は，Sb = 0.3179 である。
   
5. 平方和 Sw を求める。Sw = St - Sb の関係式から求めてもよい。
   
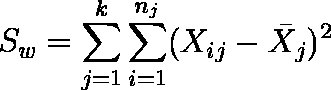
   例題の場合は，Sw = St - Sb = 0.3100 である。
   
6. 表 2 に示すような分散分析表を作る。
   

   表 2.　一元配置分散分析表

   変動要因	変動（平方和）	自由度	不偏分散（平均平方）	F 値
   群間	Sb	dfb = k - 1	Vb = Sb / dfb	F0 = Vb / Vw
   群内	Sw	dfw = n - k	Vw = Sw / dfw
   全体	St = Sb + Sw	dft = n - 1	Vt = St / dft

   
   例題の場合，以下のような分散分析表を得る。
   

   変動要因	変動（平方和）	自由度	不偏分散（平均平方）	F 値
   群間	0.3179	2	0.1589	4.6146
   群内	0.3100	9	0.0344
   全体	0.6278	11	0.0571

   
   F0 = 4.6146 となる。
   
7. 検定統計量 F0 は，第 1 自由度が dfb（ = k - 1 ），第 2 自由度が dfw（ = n - k ）の F 分布に従う。
   例題の場合，自由度は dfb= 2，dfw = 9 である。
   
8. 第 1 自由度が dfb，第 2 自由度が dfw の F 分布において，有意確率を P = Pr｛F ≧ F0｝ とする。
   F 分布表（α = 0.05，α = 0.025，α = 0.01，α = 0.005），または F 分布の上側確率の計算を参照すること。
   例題では，自由度が（2，9）の F 分布において，Pr｛F ≧ 4.26｝= 0.05　であるから，P = Pr｛F ≧ 4.6146｝＜ 0.05 である（正確な有意確率：P = 0.0417488）。
   
9. 帰無仮説の採否を決める。
   
   • P ＞ α のとき，帰無仮説を採択する。「各群の母平均値は等しくないとはいえない」。
   • P ≦ α のとき，帰無仮説を棄却する。「各群の母平均値は等しくない」。
   
   例題では，有意水準 5% で検定を行うとすれば（α = 0.05），P ＜ α であるから，帰無仮説を棄却する。すなわち，「各群の平均値は等しくない」。

ウィキペディア

一元配置分散分析

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2018/07/28 01:18 UTC 版)

統計学において、一元配置分散分析（いちげんはいちぶんさんぶんせき、英: one-way analysis of variance、略称: one-way ANOVA）は、F分布を用いて3つ以上の標本の平均を比較するために使われる手法である。この手法は数値データに対してのみ使うことができる。

ANOVAは、2つ以上の群の中の標本が同じ平均値を持つ母集団から取られた、という帰無仮説を検定する。これを行うために、2つの推定量が母集団の分散から作られる。これらの推定量は様々な仮定に依っている。ANOVA は、平均間の計算された分散と標本内の分散の比であるF統計量を生成する。もし複数の群の平均が同じ平均値の母集団から取られれば、中心極限定理にしたがって群の平均間の分散は標本の分散よりも低くなる。したがって、高い比は標本が異なる平均値を持つ母集団から取られたものであることを示唆する。

しかしながら、典型的には、one-way ANOVAは少なくとも3つ以上の群間の差の検定のために使われる。これは、2群の場合はt検定で取り扱うことができるためである。比較する平均が2つしかない時は、t検定とF検定は等価である。ANOVAとtとの間の関係はF = t²によって与えられる。One-way ANOVAの拡張は、1つの従属変数に対する2つの異なる分類の独立変数の影響を調べる二元配置分散分析である。

仮定

One-way ANOVAの結果は以下の仮定が満される限りにおいて信頼性があると見なすことができる。

• 応答関数残差は正規分布する（あるいは近似的に正規分布する）。
• 標本は独立である。
• 母集団の分散は等しい。
• 任意の群に対する応答は互いに独立で同一の分布に従う正規確率変数である（単純確率変数ではない）。

ANOVAは正規性の仮定の違反に関しては比較的頑健な手順である。もしデータが順序尺度であれば、クラスカル＝ウォリス一元配置分散分析といったノンパラメトリックな代替法を用いなければならない。

固定効果、完全ランダム化実験、非釣り合い型データの場合

モデル

正規線形モデルは、完全に同じようなベル（正規）カーブで異なる平均値の確率分布を持つ処理群を記述する。ゆえに、モデルのフィッティングは、それぞれの処理群の平均値と分散計算（処理群内の平均分散が使われる）のみを必要とする。平均と分散の計算は仮説検定の一部として行われる。

完全にランダム化された実験のための一般的に使われる正規線形モデルは

$y_{i,j}=\mu _{j}+\varepsilon _{i,j}$（平均モデル）

あるいは

$y_{i,j}=\mu +\tau _{j}+\varepsilon _{i,j}$（効果モデル）

である。上式において、

• $i=1,\dotsc ,I$は実験単位の添え字
• $j=1,\dotsc ,J$は処理群の添え字
• $I_{j}$はj番目の処理群における実験単位の数
• $I=\sum _{j}I_{j}$は実験単位の総数
• $y_{i,j}$は観測
• $\mu _{j}$はj番目の処理群の観測の平均
• $\mu$観測の総平均
• $\tau _{j}$はj番目の処理効果（総平均からのずれ）
• $\sum \tau _{j}=0$
• $\mu _{j}=\mu +\tau _{j}$
• $\varepsilon \thicksim N(0,\sigma ^{2})$, $\varepsilon _{i,j}$は正規分布したゼロ平均のランダム誤差

である。

実験単位の添え字iは複数の方法で解釈できる。一部の実験では、同じ実験単位が処理の範囲の対象となり、iは特定の単位を指す。その他では、それぞれの処理群が異なる実験単位の組を持ち、iは単純にj番目の表の添え字となる。

データとデータの統計的概要

ANOVAデータの構造化、非釣り合い型、単一因子

	群観測の一覧
	1	2	$\dotso$	$j$	$\dotso$	$J$
1	$y_{11}$	$y_{12}$				$y_{1J}$
2	$y_{21}$	$y_{22}$				$y_{2J}$
3
$\vdots$
$i$				$y_{ij}$
$\vdots$
	$y_{I_{1}1}$	$\dotso$
		$y_{I_{2}2}$	$\dotso$
	群の要約統計量						総要約統計量
観測の数	$I_{1}$	$I_{2}$	$\dotso$	$I_{j}$	$\dotso$	$I_{J}$	観測の数	$I=\sum I_{j}$
和				$\sum _{i}y_{ij}$			和	$\sum _{j}\sum _{i}y_{ij}$
平方和				$\sum _{i}(y_{ij})^{2}$			平方和	$\sum _{j}\sum _{i}(y_{ij})^{2}$
平均	$m_{1}$	$\dotso$		$m_{j}$	$\dotso$	$m_{J}$	平均	$m$
分散	$s_{1}^{2}$	$\dotso$		$s_{j}^{2}$	$\dotso$	$s_{J}^{2}$	分散	$s^{2}$

モデルと要約を比較する: $\mu =m$および$\mu _{j}=m_{j}$。総平均および総分散は、群平均と群分散からではなく、総和から計算される。

仮説検定

要約統計量を所与として、仮説検定の計算を表形式で示している。平方和の2つの列が説明値を示しているのに対して、結果の説明には1つの列しか必要ではない。

ANOVA表、固定モデル、単一因子、完全ランダム化実験

変動要因	平方和 (SS)	平方和 (SS)	自由度 (DF)	平方平均 (MS)	F
	説明SS	計算SS	DF	MS
処理	$\sum _{Treatments}I_{j}(m_{j}-m)^{2}$	$\sum _{j}{\frac {(\sum _{i}y_{ij})^{2}}{I_{j}}}-{\frac {(\sum _{j}\sum _{i}y_{ij})^{2}}{I}}$	$J-1$	${\frac {SS_{Treatment}}{DF_{Treatment}}}$	${\frac {MS_{Treatment}}{MS_{Error}}}$
誤差	$\sum _{Treatments}(I_{j}-1)s_{j}^{2}$	$\sum _{j}\sum _{i}y_{ij}^{2}-\sum _{j}{\frac {(\sum _{i}y_{ij})^{2}}{I_{j}}}$	$I-J$	${\frac {SS_{Error}}{DF_{Error}}}$
総計	$\sum _{Observations}(y_{ij}-m)^{2}$	$\sum _{j}\sum _{i}y_{ij}^{2}-{\frac {(\sum _{j}\sum _{i}y_{ij})^{2}}{I}}$	$I-1$

$MS_{Error}$は、モデルの$\sigma ^{2}$に対応する分散の推定量である。

分析の概要

中心的なANOVA解析は一連の計算から構成される。データを表形式でまとめ、次に

• それぞれの処理群は、実験単位の数、2つの和、1つの平均、1つの分散によって要約される。処理群の要約統計量が合わさり、実験単位の総数と総和が与えられる。総平均と総分散は総和から計算される。処理平均と総平均がモデルで使われる。
• 3つの自由度 (DF) および平方和 (SS) は要約統計量から計算される。次に、平方平均 (MS) が計算され、比からFが決定される。
• 計算機は通常、Fからp値を決定し、これによって処理が有意に異なる結果を生んだかどうかが決定される。もし結果が有意であれば、一時的モデルは妥当性があるとされる。

実験が釣り合い型の場合は、全ての$I_{j}$項は等しく、したがってSS式が単純になる。

実験単位（あるいは環境効果）が一様ではないより複雑な実験では、行の統計量も分析に使われる。モデルは$i$に依存した項を含む。追加項の決定は利用できる自由度の数を減少させる。

参考文献

• George Casella (18 April 2008). Statistical design. Springer. ISBN 978-0-387-75965-4. http://www.springer.com/statistics/statistical+theory+and+methods/book/978-0-387-75964-7. 

関連項目

• F検定