Cutler - Ederer 法による生命表

統計学用語辞典

Cutler - Ederer 法による生命表

　生存時間を区間に分ける場合に，各区間は等間隔でなくともよい。むしろ，各区間内では瞬間死亡率が一定であることを仮定しているので，例えば，最初の頃と後の方で瞬間死亡率が変るようならば，最初の方の区間は短く後の方の区間は長くするようなことも必要である。区間数が多すぎても少なすぎても適切な生命表は得られない。

Cutler - Ederer 法による生命表

　生命保険数理法による生命表を求める（臨床生命表とも呼ばれる。例数が少ないときには，Kaplan - Meier 法による生命表を使用すること）。


生命表の作成
　Cutler - Ederer 法では，生存期間をいくつかの区間に区分して各区間での生存率を求め，それに基づいて累積生存率を求める。

1. 生存時間を k 個の区間に分割し（注），各区間における生存数と死亡数について表にまとめる。
   表 1 のように，色の付いたセルの数値（n1 と di ，ui+wi ，i = 1, 2, ..., k ）のみがまず埋められ，残りのセルは計算によって求める。
   
2. 区間 i の開始時に生存しているケース数を ni，区間 i の終了までに死亡したケース数を di，区間 i の途中で打切られているケース数を wi，区間 i の途中で追跡不能となったケース（脱落例）数を ui とする。
   ni = ni-1 - ( di-1 + ui-1 + wi-1 ),　　i ＞ 1
   n'i = ni - (ui + wi ) / 2
   
3. 区間 i での死亡率 qi と生存率 pi は（ 1 ），（ 2 ）式で定義される（ i = 1， 2， ... ， k ）。
   （ 1 ）式でわかるように，本法では打ち切り例と脱落例を同等に扱っている。
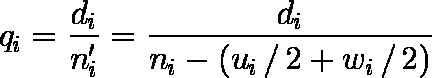   　…… ( 1 )
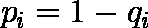   　…… ( 2 )
   
4. 区間 i 終了時の累積生存率 Pi は（ 3 ）式で定義される。
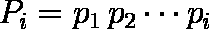   　…… ( 3 )

　表 1 および図 1 に例を示す。

表 1．Cutler - Ederer 法による生命表

区間	i	ni	di	ui+wi	ni'	qi	pi	Pi	SE(Pi)
0〜	1	37	3	8	33.0	0.09091	0.90909	0.90909	0.05004
10〜	2	26	2	3	24.5	0.08163	0.91837	0.83488	0.06813
20〜	3	21	3	1	20.5	0.14634	0.85366	0.71270	0.08735
30〜	4	17	4	4	15.0	0.26667	0.73333	0.52265	0.10356
40〜	5	9	1	0	9.0	0.11111	0.88889	0.46458	0.10711
50〜	6	8	2	0	8.0	0.25000	0.75000	0.34843	0.10729
60〜	7	6	3	0	6.0	0.50000	0.50000	0.17422	0.08909
70〜	8	3	1	0	3.0	0.33333	0.66667	0.11614	0.07600
80〜	9	2	0	0	2.0	0.00000	1.00000	0.11614	0.07600
90〜	10	2	1	0	2.0	0.50000	0.50000	0.05807	0.05595
100〜	11	1	0	0	1.0	0.00000	1.00000	0.05807	0.05595
110〜	12	1	0	0	1.0	0.00000	1.00000	0.05807	0.05595
120〜	13	1	0	1	0.5	0.00000	1.00000	0.05807	0.05595

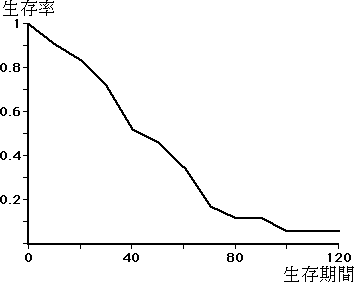図 1．Cutler - Ederer 法による生存率曲線

生存率の比較
　Cutler - Ederer 法では，各区間ごとの生存率に 2 群間で差があるかどうかを検定することができる。

1. 区間 i における 累積生存率の標準誤差 SE ( Pi ) は（ 4 ）式で求められる。
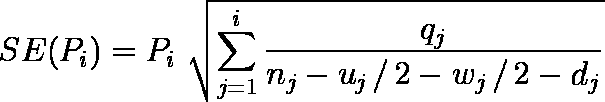   　…… ( 4 )
   
2. ある区間における A 群，B 群の累積生存率を Pa，Pb，それぞれの標準誤差を SEa，SEb としたとき，（ 5 ）式で定義される Z0 が標準正規分布に近似できることを利用する。
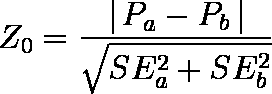   　…… ( 5 )

参考文献

1. 富永祐民: 治療効果判定のための実用統計学 − 生命表法の解説 − . 蟹書房, 東京, 1980.
   
2. Cutler, S. J. and Ederer, F.: Maximum utilization of the life table method in analysing survival. J. Chron. Dis. 8 , 699 - 712, 1958.