17
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/12/07 14:07 UTC 版)
17(十七、じゅうしち、じゅうなな)は自然数、また整数において、16の次で18の前の数である。ラテン語では septendecim(セプテンデキム)。
1/7
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/11/16 06:29 UTC 版)
1/7(7分の1、ななぶんのいち、しちぶんのいち)は、0 と 1 の間にある有理数である。
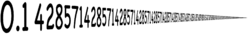
数学的性質
- 1 ÷ 7 に等しい。7 の逆数である。
- 1/7 = 0.142857142857… (下線部は循環節で長さは6)
- 1/n の形で巡回数を作る最小の数である。次は1/17。(オンライン整数列大辞典の数列 A001913)
- 円周率 π の小数部分 0.14159265… に近い。つまり、31/7 = 22/7 は π に近く、これは古代から知られる π の近似値である。(オンライン整数列大辞典の数列 A068028)
その他 1/7 に関すること
- 1954年イギリスグランプリ - このレースでは、7人のドライバー (ゴンサレス、ホートーン、マリモン、ファンジオ、モス、ベーラ、アスカリ) が1′50″のファステストラップを記録し、樹立者が複数名の場合は人数で等分されることになっていたため、7等分した1⁄7点が各ドライバーに与えられた。
符号位置
Unicodeで表記することも可能(Unicode一覧 2000-2FFF)。OS X MavericksおよびWindows 8.1では最初から表示に対応している。それ以外の環境であれば、ARIB外字をUnicodeでサポートしたフォントなどが必要。
| 記号 | Unicode | JIS X 0213 | 文字参照 | 名称 |
|---|---|---|---|---|
| ⅐ | U+2150 | - | ⅐⅐ | 7分の1 |
脚注
- ^ R. W. Barnard On Applications of Special Functions to Disparate Fields J. Analysis Volume 18 (2010), 9–2
17%
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/12/06 01:16 UTC 版)
『17%』(じゅうななパーセント)は、日本の女性歌手・渡辺美優紀の1枚目のアルバム。2019年4月3日にワーナーミュージック・ジャパン(etichetta)より発売された。
- ^ “17%|渡辺美優紀”. ORICON NEWS. oricon ME. 2021年4月29日閲覧。
- ^ “「みるきー」こと渡辺美優紀、1stソロAL『17%』JK写&アー写公開”. BARKS (イード). (2019年2月22日) 2021年4月29日閲覧。
- ^ “渡辺美優紀1stアルバムリパッケージ盤発売、つんく♂提供曲含む5曲追加収録”. 音楽ナタリー (ナターシャ). (2019年6月12日) 2021年4月29日閲覧。
- ^ a b 渡辺美優紀 2019a。
- ^ 渡辺美優紀 2019b
- ^ a b 渡辺美優紀 2019c。
あっとせぶんてぃーん
(17 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/07/16 10:21 UTC 版)
あっとせぶんてぃーん(@17、at Seventeen)は、日本の老舗メイドカフェ、@ほぉ〜むカフェの現役メイド約300人の中から選抜された日本の女性ダンス&ボーカルグループ。
注釈
- ^ 同年2月に@ほぉ〜むカフェを運営するインフィニアの親会社となったスペースシャワーネットワークのプロデュース
出典
- ^ “めいどいん!、派生4ユニットの楽曲収録1stミニALリリース&東阪で1stライブ開催決定”. 2022年12月7日閲覧。
- ^ a b “【@ほぉ〜むカフェ発メイドユニット】『@17』がTOKYO IDOL FESTIVALに出演!”. PR TIMES (2016年6月24日). 2020年11月22日閲覧。
- ^ “あっとせぶんてぃーんとは”. あっとせぶんてぃーん. 2020年11月22日閲覧。
- ^ @maid_mishina (2022年5月7日). "水色のペンライトふりふりしてもらうのが夢だったんだよ〜" (ツイート). Twitterより2022年11月20日閲覧。
- ^ @maid_emachii (2022年6月10日). "あ!えまちぃのペンライトカラーは、青💙です🪄濃い青🪄" (ツイート). Twitterより2022年11月20日閲覧。
- ^ a b “かしま卒業のお知らせ”. あっとせぶんてぃーん (2020年8月10日). 2020年11月22日閲覧。
- ^ a b “メンバーの契約解除について”. あっとせぶんてぃーん. 2020年11月22日閲覧。
- ^ “らんする~!!とは?”. らんする~!!とは? - らんする~!! ~俺がアイドルになった理由(わけ)~ (2018年9月18日). 2020年11月22日閲覧。
- ^ “あっとせぶんてぃーんオルタ 『Shining My Love』”. SPACE SHOWER MUSIC (2019年6月26日). 2020年11月22日閲覧。
- ^ “LiNK-UP、メイドカフェ「@ほぉ~むカフェ」運営会社インフィニアの全株式を売却! 売却先はスペースシャワーネットワーク”. アキバ総研 (2017年2月26日). 2018年5月16日閲覧。
- ^ “SPACE SHOWERがプロデュースする秋葉原「@ほぉ〜むカフェ」のメイドによるポップユニット「@17(あっとせぶんてぃーん)」がカジヒデキ&かせきさいだぁタッグによる新曲CDを発売!”. PR TIMES (2017年7月26日). 2018年5月16日閲覧。
- ^ “メイドカフェ発ポップユニット「@17」、メンバーが語る怒涛の初経験エピソード””. BARKS. (2017年9月13日)
- ^ a b “@ほ~むカフェから生まれたガールズポップユニット「あっとせぶんてぃーん」の新番組がはじまります。”. ニッポン放送. 2018年5月15日閲覧。
- ^ “4thシングル「毎日がジェットコースター」公式Music Video”. YouTube. (2018年4月25日)
- ^ “メイドカフェから飛び出した!!ポップユニットあっとせぶんてぃーん、ニューシングル「夏のカナリア」のMVと…”. SPACE SHOWER MUSIC. 2020年11月22日閲覧。
- ^ “あっとせぶんてぃーん新メンバーオーディション期間延長のお知らせ! 平松可奈子さんに加え、TOKYO IDOL FESTIVALの総合プロデューサーが審査員チームに参加決定”. @17 (2019年2月13日). 2020年11月22日閲覧。
- ^ “@ほぉ~むカフェ」現役メイドによるポップユニット・あっとせぶんてぃーんが、初の配信ライブを開催!”. ザテレビジョン (2020年6月5日). 2020年11月22日閲覧。
- ^ “あっとせぶんてぃーんの新曲「ダンスフラミンゴ」がお聞きいただけるのは今ここだけです…”. あっとせぶんてぃーん公式Twitter (2020年11月21日). 2020年11月22日閲覧。
- ^ “現役メイドユニット「あっとせぶんてぃーん」の2ndアルバム「risk」発売記念特番「risk & run」6月8日生放送決定”. インターエフエム (2021年6月2日). 2022年11月20日閲覧。
- ^ “ユニット兼任&メジャーデビューのお知らせ” (2021年8月14日). 2022年11月20日閲覧。
- ^ “あっとせぶんてぃーん/ドール×ドール/浪速萌々倶楽部/rurulu from めいどいん! 始動” (2022年2月15日). 2022年11月20日閲覧。
- ^ “ムテキの笑顔”. ORICON NEWS. 2020年11月22日閲覧。
- 1 あっとせぶんてぃーんとは
- 2 あっとせぶんてぃーんの概要
- 3 概要
- 4 作品
- 5 出演
- 6 脚注
丸数字
(17 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/05/03 09:25 UTC 版)
丸数字(まるすうじ)とは、数字を丸で囲っているもののことである。丸付き数字(まるつきすうじ)・丸囲み数字(まるかこみすうじ)とも呼ばれる。
- ^ 山形県民はなぜ(1)を「いちかっこ」と読むのか 専門家に見解を聞いた, Jタウンネット, 閲覧日:2021年12月04日
- ^ OSやフォントによっては、2桁の数字が1つの合成用丸に収まるレンダリングになる場合がある(例: 「42⃝」、これはWindows XPのFirefoxにて「Cambria Math」のフォントを使用すると「㊷」のような表示となるが、本来は合成用丸が1文字に対応しているため「4②」と表示されるべきである)。
囲み英数字
| 囲み英数字 | |
|---|---|
| Enclosed Alphanumerics | |
| 範囲 | U+2460..U+24FF (160 個の符号位置) |
| 面 | 基本多言語面 |
| 用字 | Common |
| 割当済 | 160 個の符号位置 |
| 未使用 | 0 個の保留 |
| Unicodeのバージョン履歴 | |
| 1.0.0 | 139 (+139) |
| 3.2 | 159 (+20) |
| 4.0 | 160 (+1) |
| 備考: [1][2] | |
囲み英数字(かこみえいすうじ、英語: Enclosed alphanumerics)は、Unicodeのブロックの一つであり、丸や括弧で囲まれた英数字やピリオドつきの数字が収録されている。この他、Unicode バージョン 6.0で追加多言語面(SMP)に囲み英数字補助ブロックが追加された。
目的
囲み英数字の多くは元々箇条書き用に使用されていた[3]。括弧で囲まれた形式は、歴史的に、丸囲みの文字をタイプライターで表現しようとした形に基づいている[3]。これらの役割は、 リッチテキストにおいてはスタイルやマークアップに置き替えられた。しかし、東アジアの既存の文字コードとの互換性や、テキストファイルでそのような記号が使用される場合のために、囲み文字がUnicode標準に含まれている[3]。Unicode規格では、著作権や商標の記号として定義されている丸囲みのC・P・Rやアットマークなど、目的に特化した文字は囲み文字とは区別している[3]。
英数字を囲むすべての文字がこの区間にあるわけではないことに注意。 Unicode区間装飾記号(Dingbat)では、U+2777からU+2793まで、数字1から10を囲む黒文字、数字1から10を囲む非セリフ文字、数字1から10を囲む非セリフ黒文字の順にある。
文字コード表
| 囲み英数字(Enclosed Alphanumerics)[1] Official Unicode Consortium code chart (PDF) | ||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
| U+246x | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ | ⑪ | ⑫ | ⑬ | ⑭ | ⑮ | ⑯ |
| U+247x | ⑰ | ⑱ | ⑲ | ⑳ | ⑴ | ⑵ | ⑶ | ⑷ | ⑸ | ⑹ | ⑺ | ⑻ | ⑼ | ⑽ | ⑾ | ⑿ |
| U+248x | ⒀ | ⒁ | ⒂ | ⒃ | ⒄ | ⒅ | ⒆ | ⒇ | ⒈ | ⒉ | ⒊ | ⒋ | ⒌ | ⒍ | ⒎ | ⒏ |
| U+249x | ⒐ | ⒑ | ⒒ | ⒓ | ⒔ | ⒕ | ⒖ | ⒗ | ⒘ | ⒙ | ⒚ | ⒛ | ⒜ | ⒝ | ⒞ | ⒟ |
| U+24Ax | ⒠ | ⒡ | ⒢ | ⒣ | ⒤ | ⒥ | ⒦ | ⒧ | ⒨ | ⒩ | ⒪ | ⒫ | ⒬ | ⒭ | ⒮ | ⒯ |
| U+24Bx | ⒰ | ⒱ | ⒲ | ⒳ | ⒴ | ⒵ | Ⓐ | Ⓑ | Ⓒ | Ⓓ | Ⓔ | Ⓕ | Ⓖ | Ⓗ | Ⓘ | Ⓙ |
| U+24Cx | Ⓚ | Ⓛ | Ⓜ | Ⓝ | Ⓞ | Ⓟ | Ⓠ | Ⓡ | Ⓢ | Ⓣ | Ⓤ | Ⓥ | Ⓦ | Ⓧ | Ⓨ | Ⓩ |
| U+24Dx | ⓐ | ⓑ | ⓒ | ⓓ | ⓔ | ⓕ | ⓖ | ⓗ | ⓘ | ⓙ | ⓚ | ⓛ | ⓜ | ⓝ | ⓞ | ⓟ |
| U+24Ex | ⓠ | ⓡ | ⓢ | ⓣ | ⓤ | ⓥ | ⓦ | ⓧ | ⓨ | ⓩ | ⓪ | ⓫ | ⓬ | ⓭ | ⓮ | ⓯ |
| U+24Fx | ⓰ | ⓱ | ⓲ | ⓳ | ⓴ | ⓵ | ⓶ | ⓷ | ⓸ | ⓹ | ⓺ | ⓻ | ⓼ | ⓽ | ⓾ | ⓿ |
備考
| ||||||||||||||||
絵文字
このブロックには、1文字の絵文字(U+24C2)が収録されている[4][5]。これは丸囲みのMで、地下鉄(metro)を表す[6]。また、マスクワーク(半導体デバイスのチップ上の配置)を表す[7]。
この文字に対し2種類の異体字セレクタ、絵文字表示(U+FE0F VS16)かテキスト表示(U+FE0E VS15)が適用できる。デフォルトはテキスト表示である[8]。
| U+ | 24C2 |
| base code point | Ⓜ |
| base+VS15 (text) | Ⓜ︎ |
| base+VS16 (emoji) | Ⓜ️ |
履歴
以下の表に挙げられているUnicode関連のドキュメントには、このブロックの特定の文字を定義する目的とプロセスが記録されている。
| バージョン | コードポイント[a] | 文字数 | L2 ID | WG2 ID | ドキュメント |
|---|---|---|---|---|---|
| 1.0.0 | U+2460..24EA | 139 | (to be determined) | ||
| L2/11-438[b][c] | N4182 | Edberg, Peter (2011-12-22), Emoji Variation Sequences (Revision of L2/11-429) | |||
| 3.2 | U+24EB..24FE | 20 | L2/99-238 | Consolidated document containing 6 Japanese proposals, (1999-07-15) | |
| N2093 | Addition of medical symbols and enclosed numbers, (1999-09-13) | ||||
| 4.0 | U+24FF | 1 | L2/01-480 | Muller, Eric (2001-12-14), Proposal to add NEGATIVE CIRCLED DIGIT ZERO | |
| L2/02-193 | Muller, Eric (2001-12-14), Proposal to add Negative Circled Digit Zero | ||||
関連項目
- 囲み文字
- 著作権マーク、登録商標マーク、レコード著作権マークはこのブロックではないところで別に定義されている。
- en:Japanese rebus monogram(日本の判じ物モノグラム)
出典
- ^ “Unicode character database”. The Unicode Standard. 2016年7月9日閲覧。
- ^ “Enumerated Versions of The Unicode Standard”. The Unicode Standard. 2016年7月9日閲覧。
- ^ a b c d The Unicode Standard, 6.0.1
- ^ “UTR #51: Unicode Emoji”. Unicode Consortium (2016年11月22日). 2016年12月22日閲覧。
- ^ “UCD: Emoji Data for UTR #51”. Unicode Consortium (2016年11月14日). 2016年12月22日閲覧。
- ^ “Ⓜ️ Circled Latin Capital Letter M Emoji”. 2018年1月27日閲覧。
- ^ “Federal Statutory Protection for Mask Works (Copyright Circular 100)”. 合衆国著作権局. pp. 5 (2012年9月). 2014年3月22日閲覧。
- ^ “Unicode Character Database: Standardized Variation Sequences”. The Unicode Consortium. 2016年12月22日閲覧。
正の数と負の数
(17 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/02/01 01:43 UTC 版)
数学における正の数(せいのすう、英: positive number, plus number, above number; 正数)は、0より大きい実数である。対照的に負の数(ふのすう、英: negative number, minus number, below number; 負数)は、0より小さい実数である。とくに初等数学・算術や初等数論などの文脈によっては、(暗黙の了解のもと)特に断りなく、より限定的な範囲の正の有理数や正の整数という意味で単に「正の数」と呼んでいる場合がある。負の数も同様である。
- ^ 『相対論の式を導いてみよう、そして、人に話そう』(小笠英志、ベレ出版、ISBN 978-4860642679)の PP.121-127にマイナス×マイナスがプラスになることの小学生も納得できる説明が書いてある。
- ^ Hayashi, Takao (2005), "Indian Mathematics", in Flood, Gavin, The Blackwell Companion to Hinduism, Oxford: Basil Blackwell, 616 pages, pp. 360-375, ISBN 978-1-4051-3251-0.
- ^ Colva Roney-Dougal, Lecturer in Pure Mathematics at the University of St Andrews, stated this on the BBC Radio 4 "In Our Time", on Negative Numbers, 9 March 2006.
- ^ Knowledge Transfer and Perceptions of the Passage of Time, ICEE-2002 Keynote Address by Colin Adamson-Macedo. [1]
- ^ Maseres, Francis, 1731–1824. A dissertation on the use of the negative sign in algebra, 1758.
- ^ Alberto A. Martinez, Negative Math: How Mathematical Rules Can Be Positively Bent, Princeton University Press, 2006; おもに1600年代から1900年代前半にかけての、負数に関する論争の歴史。
#17
17
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/11/03 22:15 UTC 版)
「世界の終わりと夜明け前」の記事における「17」の解説
初出:『週刊ビッグコミックスピリッツ増刊casual』第17号(2008年2月15日発行) 高校生の田村は、ある日、コンビニエンスストアで態度の悪い店員に腹を立て、開きっぱなしのレジスターから現金3万円を盗んでしまう。金の使い道を考えながら街を歩いていると、同じ高校に通う女子と見知らぬ男子が言い争っているのを目撃する。女子が一人になったところで田村は彼女に話しかける。その女子には金を払えば性交を行わせてくれるという噂が流れており、田村は「3万円を支払うからヤラせてくれないか」と持ちかける。女子は田村を罵倒してその場を去る。その夜、TVで自分が現金を盗んだコンビニエンスストアに強盗が押し入り、現金数十万円を盗んだというニュースが流れ、田村は自分の罪がなかったことになってしまったのを悟る。翌日田村は件のコンビニへ立ち寄り、盗んだ3万円を募金箱へ入れて退店する。その後遅刻して登校し、昨日話した女子生徒と目が合うがすぐに逸らされてしまった。 登場人物 田村 眼鏡をかけた細身の高校生男子。自身の未来について虚無的に考える。何事に対しても内心で毒づいている。同級生から文化祭でバンドをやらないかと持ちかけられ、親から金を借りてサンプラーを購入する。 女子生徒 田村とは違うクラスの女子生徒。AV女優の森川汁子と容姿が似ており、金を払えば性交をさせてくれるという噂が校内で流れている。
※この「17」の解説は、「世界の終わりと夜明け前」の解説の一部です。
「17」を含む「世界の終わりと夜明け前」の記事については、「世界の終わりと夜明け前」の概要を参照ください。
17
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/05/10 16:45 UTC 版)
語り部の一人。インターネット上にしか姿を現さない。徳永とともに<<完璧な場所>>で自殺しようとしている。
※この「17」の解説は、「15×24」の解説の一部です。
「17」を含む「15×24」の記事については、「15×24」の概要を参照ください。
17
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/05/13 01:40 UTC 版)
イタリアでは 17 が忌み数とされる。17 をローマ数字で書くと XVII となり、これを並べ替えると VIXI となる。ラテン語で vīxī は、vīvō 「私は生きている」の直説法完了にあたり、「私は生きることを終えた(私は死んでいる)」という意味になるからである。 13 と同様に、建物の階や部屋番号などにおいて飛ばされることがある。その他、イタリアの航空会社アリタリア航空の航空機には客席に「17列」が存在しない。フランスの自動車会社ルノーは「R17」という車種を、イタリア向けには「R177」として販売している。
※この「17」の解説は、「忌み数」の解説の一部です。
「17」を含む「忌み数」の記事については、「忌み数」の概要を参照ください。
17
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/12/17 15:48 UTC 版)
旧・両備鉄道 → 神高鉄道 9 - 1924年、独オーレンシュタイン・ウント・コッペル製 - 車軸配置0-6-0 (C)。買収後ケ217形 217
※この「17」の解説は、「佐世保鉄道」の解説の一部です。
「17」を含む「佐世保鉄道」の記事については、「佐世保鉄道」の概要を参照ください。
17
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/04/03 19:07 UTC 版)
「JR貨物UT9C形コンテナ」の記事における「17」の解説
日本陸運産業(NRS)所有/新日鐵化学借受。※ 保護枠なし。
※この「17」の解説は、「JR貨物UT9C形コンテナ」の解説の一部です。
「17」を含む「JR貨物UT9C形コンテナ」の記事については、「JR貨物UT9C形コンテナ」の概要を参照ください。
17
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/05/20 17:54 UTC 版)
ヤクルト、DeNAではエースナンバーとしている。 ヤクルトでは宮地惟友→佐々木重徳→鈴木皖武→松岡弘→川崎憲次郎→川島亮→クリス・ラルー→成瀬善久→清水昇の9名のみが使用している(ただし佐々木は野手である)。 DeNAでは秋山登→山下律夫→斉藤明夫→盛田幸希→加藤武治→清水直行→三嶋一輝が着用する。大洋時代から受け継がれ、現在までに使用した選手も前述の選手を含め9名である。 他球団ではビクトル・スタルヒン、藤本英雄、山田久志、完全試合を達成した槙原寛己らがおり、現役では増井浩俊(オリックス)、柳裕也(中日)などがいる。 一軍で実績を残した打者での着用例は前述の佐々木の他、桑野議(阪神・外野手)、門前眞佐人(阪神・大洋・広島、捕手)など少数である。 ロッテ・佐々木朗希は2022年4月10日に、オリックス戦で1試合19奪三振と13者連続奪三振を記録。日本新記録と日本記録タイを獲得した。完全試合達成者
※この「17」の解説は、「エースナンバー」の解説の一部です。
「17」を含む「エースナンバー」の記事については、「エースナンバー」の概要を参照ください。
「17」の例文・使い方・用例・文例
- おそらく17世紀最高の英国作家といえるジョン・ミルトン
- 彼女はバースデーケーキの上にある17本のろうそくをすべて吹き消した
- ロット17番はビクトリア様式のテーブルです
- 17ページ
- 発車は17時10分だ
- 17ドルのシャツ
- 17世紀初頭に
- 20から3を引けば17になる
- 「背の高さはどれぐらいですか」「170センチです」
- イングランドとスコットランドは1707年に合併した
- Bryce Rollins の回顧展が、6 月17 日から9 月15 日までSchulz美術館にて、同美術館の35 周年を祝って行われる。
- この映画は17世紀のあるカストラートの話である。
- 彼は1765年に王位についた。
- メゾチント彫法は17世紀に発明された。
- 福音伝播協会は1701年に英国で設立された。
- 社長から、原油の輸入を現状から少なくとも17%は減らすべきだとの指示があった。
- 千七百二十九万八千(1700,298,000)
- 私の仕事は17時までです。
- 進捗状況表を火曜日の17時までに提出してください。
- 717号室に配達されます。
「17」に関係したコラム
-
ETFの銘柄数は2012年9月の時点で約140あります。そして、いずれの銘柄にも価格の連動となる対象の商品があります。ここでは、ETFの銘柄をジャンルごとに紹介します。表の「コード」は株式コード、「市...
-
株365の取引時間は、銘柄により異なります。日経平均株価(日経225)を基準にした日経225証拠金取引(NKY/JPY)の取引時間はほぼ24時間です。他の銘柄についてはさまざまで、ニューヨークのサマー...
-
CFDの取引時間は商品内容や取引国によりさまざまです。一般的には、金や原油といったコモディティ、日本やアメリカ合衆国などの株価指数などはほぼ24時間の取引が可能です。一方、各国の株式や日米を除く株価指...
-
ETFを上場するには、証券取引所の定める上場審査基準や適時開示基準、上場廃止基準といったさまざまな基準をクリアする必要があります。2012年9月現在、ETFを上場している企業は17社あります。上のグラ...
-
ETFの取引単位は銘柄により異なります。ETFの場合、取引単位は10株単位や100株単位であることが多いようです。また、価格が1万円前後の銘柄は1株単位、100円前後の銘柄は1,000株単位が多いよう...
-
株365のギャップリスクとは、取引時間外のイベントによる急激な値動きの危険性のことです。イベントの内容は、経済指標、政変や紛争、要人の発言、為替動向などが挙げられます。例えば、日経225証拠金取引の取...
- >> 「17」を含む用語の索引
- 17のページへのリンク


