指数平滑法
【英】:exponential smoothing
概要
時系列データに対してウエイト付け平均を行って平滑化する方式で, 過去にさかのぼる程小さくなる指数型のウエイト付けを採用している. 時系列を逐次平滑化している基本式(定数型モデル)は,
 で表わされる. ここで,
で表わされる. ここで,  は
は 時点のウエイト付けされた平均値(推定値),
時点のウエイト付けされた平均値(推定値), 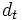 は
は 時点のデータ,
時点のデータ, 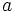 は平滑化定数(
は平滑化定数(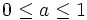 )である. また, 時系列データに傾向や季節変動がある場合の直線型傾向モデルや季節型モデルも開発されている.
)である. また, 時系列データに傾向や季節変動がある場合の直線型傾向モデルや季節型モデルも開発されている.
詳説
時間の変化に従って与えられるデータ群, すなわち, 時系列データ (例えば需要量系列など) を用いた予測方式の共通点は, 先行するデータ群をつぎに続くデータ群に関連づけて推定を行うことである. この方法の一つで指数平滑法の基礎となる方式が移動平均法である. いま,  時点の移動平均値を
時点の移動平均値を , 用いられるデータ群の項数を
, 用いられるデータ群の項数を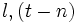 時点のデータを
時点のデータを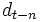 とし,
とし, 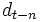 の係数を
の係数を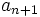 とすれば,
とすれば, 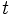 時点の移動平均値
時点の移動平均値 は次式で表される.
は次式で表される.
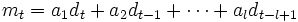
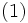
ただし, 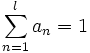
さて, 指数平滑法([1], [2])はこの(1)式の係数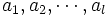 に対して, 現在時点に近い程ウエイトを大きくし, 過去にさかのぼる程ウエイトを小さくしていく指数型の考え方を導入したもので, 指数型加重移動平均法とも呼ばれている. すなわち, この方式による
に対して, 現在時点に近い程ウエイトを大きくし, 過去にさかのぼる程ウエイトを小さくしていく指数型の考え方を導入したもので, 指数型加重移動平均法とも呼ばれている. すなわち, この方式による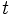 時点の推定値
時点の推定値 は次式のように表わされる. (ただし,
は次式のように表わされる. (ただし, 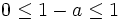 )
)
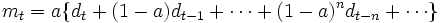
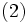
この(2)式の重み係数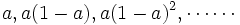 の総計は1となる. なお, この場合の
の総計は1となる. なお, この場合の は
は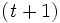 時点の予測値として用いられる. ここで, (2)式と同様な考え方で
時点の予測値として用いられる. ここで, (2)式と同様な考え方で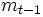 を算出すると次式が得られる.
を算出すると次式が得られる.
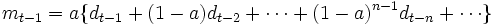
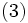
(3)式の両辺に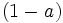 を掛けて(2)式と対比すると, 次式のような指数平滑法の基本式(定数型モデル)が導出される.
を掛けて(2)式と対比すると, 次式のような指数平滑法の基本式(定数型モデル)が導出される.

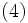
上記の平滑化定数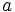 は, 原則として, 0と1の間の値をとる. この中,
は, 原則として, 0と1の間の値をとる. この中, 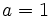 のときは
のときは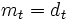 となり推定値は同時点のデータと等しくなる. 一方,
となり推定値は同時点のデータと等しくなる. 一方,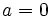 のときは
のときは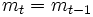 となり推定値は一時点前の先行する推定値と等しくなる.
となり推定値は一時点前の先行する推定値と等しくなる. 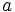 を中間の値
を中間の値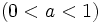 にとった場合にはある程度ランダムな変動の影響を受けることになる.
にとった場合にはある程度ランダムな変動の影響を受けることになる. 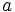 の値を最適に決めることは難しい問題であるが, 0.5より若干小さい値をとる場合が比較的多い.
の値を最適に決めることは難しい問題であるが, 0.5より若干小さい値をとる場合が比較的多い.
時系列データに傾向がない定数型モデルの場合には, (4)式の が
が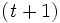 時点の有効な予測値となるが, もし, 上昇, あるいは下降の傾向がある場合は, この値は不満足なものになる. この問題を解決するために傾向を考慮した指数平滑法(直線型傾向モデル)が提案されている. このモデルでは2番目の変数として
時点の有効な予測値となるが, もし, 上昇, あるいは下降の傾向がある場合は, この値は不満足なものになる. この問題を解決するために傾向を考慮した指数平滑法(直線型傾向モデル)が提案されている. このモデルでは2番目の変数として 時点の傾向の推定値r_tを導入している. この直線型傾向モデルはR. G. Brown[3], [4] により提示されたが, いま,
時点の傾向の推定値r_tを導入している. この直線型傾向モデルはR. G. Brown[3], [4] により提示されたが, いま, 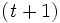 時点の予測値を
時点の予測値を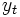 とすれば(5)~(7)式のように表わされる.
とすれば(5)~(7)式のように表わされる.
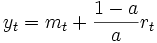
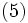

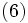
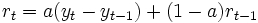
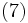
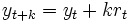
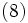
なお, (4)式や(5)式などで用いられている や
や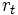 の初期値は, それまでのデータにより推定される. それらの値はとくに重要な値ではないので比較的単純な近似法を用いればよい.
の初期値は, それまでのデータにより推定される. それらの値はとくに重要な値ではないので比較的単純な近似法を用いればよい.
時系列データに季節変動がある場合には, 季節型モデルが利用される. このモデルの代表的なものはP. R. Winters [5] によって提示されているが, いま, 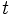 時点の季節変動指数値
時点の季節変動指数値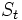 , 3つの平滑化定数をそれぞれ
, 3つの平滑化定数をそれぞれ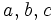 とすればこのモデルは(9)~(11)式のように表わされる.
とすればこのモデルは(9)~(11)式のように表わされる.
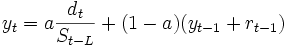
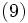
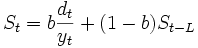
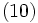
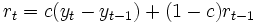
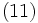
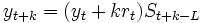
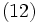
5. その他の指数平滑法
上記以外のモデルとしては, 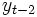 までを用いた2次のモデルや定数型モデルの推定値をデータとして同じモデルを繰り返し用いる2重や3重のモデルも提案されている.
までを用いた2次のモデルや定数型モデルの推定値をデータとして同じモデルを繰り返し用いる2重や3重のモデルも提案されている.
[1] I. C. I Monograph, No.2, Short-Term Forecasting, Imperial Chemical Industries Limited, 1964.
[2] C. C. Holt, Forecasting Seasonals and Trends by Exponentially Weighted Moving Averages, Carnegie Institute of Technology, Pittsburgh, Pennsylvania, 1957.
[3] R. G. Brown, Statistical Forecasting for Inventory Control, McGraw-Hill, 1959.
[4] R. G. Brown and R. F. Meyer, "The Fundamental Theorem of Exponential Smoothing," Operations Research, 19 (1961), 673-685.
[5] P. R. Winters, "Forecasting Sales by Exponentially Weighted Moving Averages," Management Science, 6 (1960), 324-342.
- 指数平滑法のページへのリンク
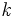
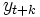 は次式のように
は次式のように は
は