数量化I類

統計学用語辞典

数量化 I 類

　連続変数である従属変数を予測する。
　ダミー変数を用いる重回帰分析と等価な解析手法である（解説）。


　説明変数 Xi（ i = 1， 2， ... ， p ）が，それぞれ mi 個の選択肢を持つ（ このような変数を特にアイテム変数と呼ぼう ）。各選択肢が選ばれたら 1，選ばれなかったら 0 をとるような Σ mi 個の変数 Cij（ i = 1， 2， ... ， p； j = 1， 2， ... ， mi ）を定義する。
　ここで，各カテゴリーに特定の数値 aij（ i = 1， 2， ... ， p； j = 1， 2， ... ， mi ）を 割当て， = Σ Σ aij Cij で従属変数 Y を予測しようと考える。

表 1．カテゴリー変数を説明変数として従属変数を予測する

従属変数 （連続変数）		説明変数（カテゴリー変数）
		X1				X2					X3
Y		C11	C12	C13		C21	C22	C23	C24		C31	C32
31.3		1	0	0		0	1	0	0		0	1
25.1		0	1	0		1	0	0	0		1	0
34.7		1	0	0		0	0	1	0		1	0
29.6		0	0	1		0	0	0	1		0	1
：
カテゴリーに 与えられる数値		a11	a12	a13		a21	a22	a23	a24		a31	a32

　表 1 に示した例においてみてみると，例えば 1 番目のケースの従属変数の観察値 31.3 の予測値として a11 + a22 + a32 を使用するわけである。
　各カテゴリーにどのような数値を与えたらよいかは，Cij を独立変数として以下のような重回帰式を求めることに帰着できる。

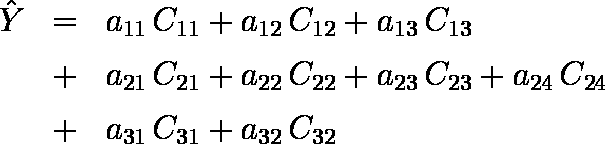
　ただし，各説明変数において情報が冗長である（ 例えば，C11 と C12 が 0 ならC13 が 1 であることはただちにわかる ）ので，2 番目以降の各説明変数から 1 個ずつカテゴリーを消去して解を求める（ダミー変数を用いて重回帰分析を行うときには，各説明変数から 1 個ずつカテゴリーを消去して分析を行う）。

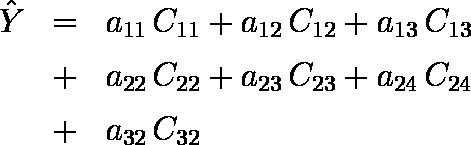
　なお，以上で求めた各カテゴリーに与える数値は，各説明変数ごとに平均値がゼロになるように正規化されて利用される。
補足説明

1. 連続変数をカテゴリー化して用いる場合には，カテゴリー数が少なすぎないようにしなければならない（ 多すぎても困る ）。また，カテゴリー化は妥当な分割点で行ったほうがよい（ 例えば 2 峰性データならその中点，正常範囲が決っているならその前後など ）。
   
2. 得られた予測式は，分析に使用したケースについて最適のものであるが，別のケース群に適用しても有用であるかどうかはわからない。例えば，ある医療機関に受療した患者に適用できても，別の医療機関の受療患者には適用できないかもしれない。得られた予測式が他の集団でも有用であるかどうか（交差妥当性を持つかどうか）について検討したほうがよい。
   
3. 交差妥当性を検証するのはなかなかたいへんな場合がある。そのため，便法として折半法と呼ばれる方法がある。この方法は，既存のケースを無作為に半分ずつに分け，一方のケースを用いて予測式を作り，もう一方のケースを得られた予測式で予測し予測式の有用性を検討するものである。折半法を用いるには，既存のケース数がある程度多くなければならない。