内心

デジタル大辞泉

ない‐しん【内心】

読み方：ないしん

１ 表に出さない気持ち。心のうち。心中。副詞的にも用いる。「—を打ち明ける」「—びくびくだった」

２ 三角形の内接円の中心。三つの内角それぞれの二等分線が交わる点に一致する。⇔外心。

算数用語集・数学用語集

（三角形の）内心

三角形の3つの内角の2等分線は1点（内心）で交わり、その点から3辺までの距離は等しい。（定理）

三角形の内心はその三角形の内接円の中心である。

参考

• 外心

ウィキペディア

内接円

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/12/19 12:31 UTC 版)

「（円に）内接する円（英語版）」とは異なります。

五角形とその内接円

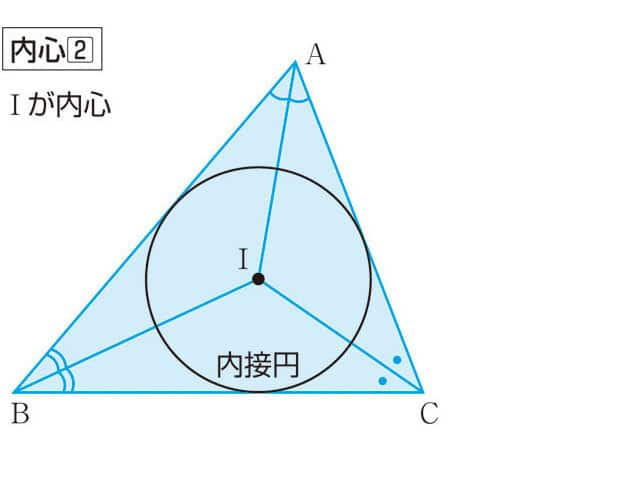
初等幾何学において、与えられた多角形の内接円（ないせつえん、英: incircle）は、その多角形に内接 (inscribe) する—この場合はその多角形の内部にあり全ての辺に接する—円を言う。内接円の中心を内心 (incenter) という。

全ての多角形に内接円が存在するわけではないが、全ての三角形と正多角形には内接円が存在する。内接円が存在する場合、その多角形の内部にある最大面積の円になる。

三角形の内接円

三角形の内接円と角の二等分線

三角形において、ある頂点と、その対辺の垂直二等分線の延長線上にある外接円(円周)との交点（対辺からみて三角形の外側の方）を結ぶ直線は、 その頂点の内角を二等分する直線となっている。（図中に緑の直線で示される。それらの交点は当該三角形の内接円の中心となっている。）

辺ＡＢＣで構成される三角形について、Ａを「当該三角形の内心からの垂線」との交点で分割してできる長さそれぞれの辺を持つ正方形同士の面積差（絶対値）は、Ａの長さと「ＢとＣの長さの差（絶対値）」との積と等しくなる。

三角形の内接円の〔半径〕は、『三種類の「頂点から内接円との接点までの距離」の辺を持つ直方体』と同じ体積の『同じ三角形を面に持つ柱』の〔高さ〕と等しくなる。

→詳細は「三角形の内接円と傍接円」を参照

任意の三角形に内接円が存在する。内心は3つの角の二等分線の交点である。

内接円の他に、三角形の外部に1辺と2辺の延長線に接する円が存在する。これを傍接円という。傍接円は1つの三角形に対し3つ存在する。

四角形の内接円

四角形に内接円が存在する必要十分条件は

• 全ての内角が180度以下
• AB + CD = BC + DA

である。凧形・菱形などが該当する。

内接円の中心と2本の対角線の中点は、同一直線上にある（ニュートンの定理）。

内接円・外接円の両方を持つ四角形を双心四角形という。

一般の多角形の内接円

多角形に内接円が存在する場合、その半径は

半径 = 2 × 面積 ÷ 周長

で求められる。

関連項目

• 外接円
• 三角形の中心
• パッキング問題（充填問題）

外部リンク

• Weisstein, Eric W. "Incircle". mathworld.wolfram.com (英語).
• Weisstein, Eric W. "Incenter". mathworld.wolfram.com (英語).
• incircle - PlanetMath.（英語）
• incenter - PlanetMath.（英語）
• Definition:Incircle at ProofWiki

この項目は、初等幾何学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています。

• 表示
• 編集

ウィキペディア小見出し辞書

内心

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/06/09 16:05 UTC 版)

「三角形」の記事における「内心」の解説

三角形の 3 つの内角の二等分線は 1 点で交わる。この点のことを内心という。内心は 3 つの辺から等距離であり、内心を中心として半径がその距離である円は 3 つの辺に接する。この円のことを内接円という。

Wiktionary日本語版（日本語カテゴリ）

内心

出典:『Wiktionary』 (2021/08/15 01:56 UTC 版)

名詞

内 心（ないしん）

1. 心の中。
2. 多角形の全ての辺に接する円の中心。

発音^(?)

な↗いしん

関連語

• 内接
• 内接円
• 外心
• 重心
• 垂心
• 傍心

Weblio日本語例文用例辞書

「内心」の例文・使い方・用例・文例

• 彼女は内心罪の意識があった
• 彼女に来てくれと頼んだものの，内心は来てほしくなかった
• その出来事のさなかにあってさえ彼は内心落ち着いていた
• 内心は真実を知っている
• 彼女は内心はその男のことが嫌いだ
• 私は内心、別のことを考えていた。
• 彼女は関心のないような顔をしているが、内心はとても喜んでいるようだ。
• 彼は自信ありげに見えたが、内心は全然違っていた。
• 政治家は決して内心を見せない。
• 内心では, 腹では.
• 心の中で, 内心.
• 彼は彼女の行状に愛想がつきたと口では言ってはいるが, さりとて内心では彼女を諦め切れないでいるように僕には思われる.
• 内心びくびくしていた.
• その表情からは彼女の内心の揺れが少しも読み取れなかった.
• 外面菩薩の如し内心夜叉の如し
• 外面菩薩の如く内心夜叉の如し
• 心ひそかに、心中ひそかに、内心ひそかに
• 彼女は自分の夫くらい偉い人は無いと内心ひそかに信じている