複数個の相関係数の同等性の検定と母相関係数の点推定

統計学用語辞典

複数個の相関係数の同等性の検定と母相関係数の点推定

例題：
　「表 1 に示す 5 個の標本相関係数について同等性の検定を行い，もし同等とみなせるならば母相関係数の点推定値を求めなさい。」

表 1．5 個の相関係数

標本の大きさ	標本相関係数
10	0.658
16	0.285
8	0.569
29	0.427
36	0.374

母相関係数の同等性の検定は以下のように行う。

1. 前提
   • 帰無仮説 H0：「母相関係数は全て等しい　ρ1=ρ2=...=ρk=ρ」
   • 対立仮説 H1：「母相関係数は異なる（帰無仮説の等号が少なくとも一つは成り立たない）」。
   • 有意水準 α で両側検定を行う（二つの相関係数の差の検定の場合には片側検定も可能）。
   
   
2. 第 i 標本のケース数および標本相関係数 を ni，ri とし，Vi=（ni - 3）とする。
   
3. k 個の標本相関係数の Z 変換値を Zi とする。
   

   表 2．複数個の相関係数の同等性の検定と母相関係数の点推定

   ni	ri	Vi	Zi	Vi Zi	Vi Zi2
   10	0.658	7	0.78928	5.52495	4.36072
   16	0.285	13	0.29312	3.81050	1.11692
   8	0.569	5	0.64604	3.23021	2.08686
   29	0.427	26	0.45622	11.86177	5.41160
   36	0.374	33	0.39307	12.97116	5.09852
   	合計	84	2.57772	37.39860	18.07461

4. 次式により，検定統計量 χ²0 を求める（ΣViZi²，ΣViZi，ΣVi は，表 2 の合計行にある）。
   
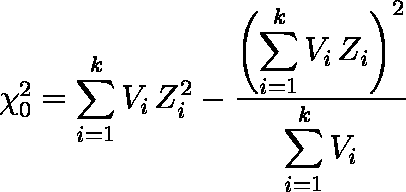
   例題では，χ²0 = 1.42396 となる。
   
5. χ²0 は，自由度が k - 1 の χ² 分布に従う。
   例題では，自由度 4 の χ² 分布に従う。
   
6. 有意確率を P = Pr｛χ² ≧ χ²0｝とする。
   χ²分布表，またはχ²分布の上側確率の計算を参照すること。
   例題では，自由度 4 の χ^2 分布において，Pr｛χ² ≧ 9.49｝= 0.05 であるから，P = Pr｛χ² ≧ 1.42396｝＞ 0.05 である（正確な有意確率：P = 0.84002）。
   
7. 帰無仮説の採否を決める。
   
   • P ＞ α のとき，帰無仮説を採択する。「母相関係数が異なるとはいえない」。
   • P ≦ α のとき，帰無仮説を棄却する。「母相関係数は異なる」。
   
   例題では，有意水準 5% で検定を行うとすれば（α = 0.05），P ＞ α であるから，帰無仮説を採択する。すなわち，「母相関係数は異なるとはいえない」。

同等性の検定で帰無仮説が採択されたときには，k 個の標本相関係数に基づいて 1 個の母相関係数を推定できる。
母相関係数の点推定は以下のように行う。

1. 次式により，k 個の標本相関係数の Z 変換値の重み付け平均値 Zm を求める（ΣViZi，ΣVi は，表 2 の合計行にある）。
   
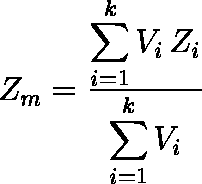
   例題では，Zm = 0.44522 である。
   
2. フィッシャーの Z 変換の逆変換（次式）により，母相関係数の点推定値 f ^-1 ( Zm ) を得る。
   
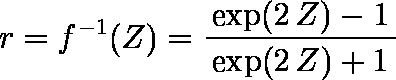
   例題では，点推定値は f ^-1 (0.44522) = 0.41796 となる。