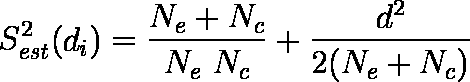複数の研究結果から effect size を統合する手法(1)
二群の平均値の差を検討するような研究では,平均値(M),標準偏差(SD),サンプルサイズ(N) という情報も提供される。
- 個々の研究における effect size は,処理群の平均値(Me)と対照群の平均値(Mc)の差を,標準偏差で割ったもので表される。これは,測定単位には無関係で,標準化された効果の大きさを表す。
- effect size g Glass(1976)
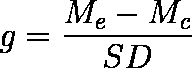
SD は,対照群の標準偏差(SDc)でもよいが,多くの場合は
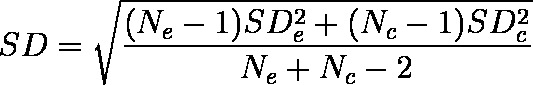
が使われる。
- effect size g は不偏推定量ではない。不偏推定量は以下の式で求められる。
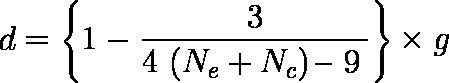
- effect size g Glass(1976)
- 全ての研究結果を統合した effect size は以下のようになる。
これを AWK スクリプトで書いてみると以下のようになる。
---------- begin # effect size の統合 平均値の差 BEGIN { k = mean_g = mean_d = sum1 = sum2 = 0 printf "%10s%10s%10s ", "M", "SD", "N" # 処理群 printf "%10s%10s%10s ", "M", "SD", "N" # 対照群 printf "%10s%10sn", "g", "d" while (getline > 0) { printf "%10g%10g%10g ", $1, $2, $3 printf "%10g%10g%10g", $4, $5, $6 s2 = sqrt((($3-1)*$2^2 + ($6-1)*$5^2) / ($3+$6-2)) g = ($1-$4)/s2 d = (1-3/(4*($3+$6)-9))*g est_s2 = ($3+$6)/($3*$6)+d^2/(2*($3+$6)) sum1 += d/est_s2 sum2 += 1/est_s2 printf " %10g%10gn", g, d k++ mean_g += g mean_d += d } print "" print "average of effect sizes" print "g =", mean_g/k print "d =", mean_d/k print "d+ =", sum1/sum2 } ---------- end
テストデータは,各研究で得られた,処理群と対照群の平均値,標準偏差,標本サイズ。 このデータは,前のページ(no01, no02)で使った P 値のデータの元になったものである。
---------- begin 130 15 10 140 20 5 120 12 40 140 15 20 140 20 30 150 25 30 160 20 40 145 35 20 ---------- end得られる結果は,
---------- begin M SD N M SD N g d 130 15 10 140 20 5 -0.598849 -0.563623 120 12 40 140 15 20 -1.53152 -1.51163 140 20 30 150 25 30 -0.441726 -0.435989 160 20 40 145 35 20 0.579389 0.571864 average of effect sizes g = -0.498178 d = -0.484846 d+ = -0.408965 ---------- endmeta-analysis により,「処理群は対照群に比べて,標準偏差のほぼ半分に相当するだけ平均値が低い」ということがわかる。単に,P 値を統合した結果(no01, no02)よりは有用な情報を引き出している。
複数の研究結果から effect size を統合する手法(2)
effect size がわかったとして,「この結果は信頼できるか」ということが問題になる。
no04 で使ったデータは非常に不均一である。この不均一性はどこから来るのか。
- random effects model (Hedges & Olkin, 1985)
観察された effect size の変動を二つの部分に分割する。
observed variance = population variance + sampling error
そして,

の値が 100% になるということは,データは均一であることを表す(望ましい状態)。
たとえば,この値が 40% であったとすると,系統的な要因による変動が 60% あることを意味するので,meta-analysis は moderator variables について検討することになる。
no04 のデータでは,d の分散(不偏分散を指しているらしい)は 0.73 でsampling error は 0.14 なので,population variance は 0.59 となる。sampling error は,わずか 19% くらいにしか過ぎないので,meta-analysis では,系統的な要因を検討する必要があることを示す。(ここのところは,Hedges &Olkin, 1985 の引用があるだけで数式が示されていない)。
とっかかりとしては,effect size の大きさにより,研究をグループ化するとよい。例では,1,3番目の研究,2番目,4番目の研究の3つのクラスターに分けられる。
- faile-safe N formula for d value Orwin(1983)
population effect size delta が 0.2 以下になってしまうには,あといくつの「no effect studies」が必要かという推定値。
no04 の例では,delta = 0.47 であるが,後 6 つの,「ネガティブデータ」が加わると delta は 0.2(これは慣用的な基準)以下になってしまう。(ここのところも,Oewin の引用のみで,数式の提示はない)。
参考文献
- Hedges, L. V. & Olkin, I. (1985). Statistical methods for meta-analysis.
New York: Academic Press.
- Orwin, R. G. (1983). A fail safe N for effect size in meta-analysis.
Journal for Educational Statistics, 8, 157-159.
- 複数の研究結果から effect size を統合する手法のページへのリンク