複数の検定結果を統合する手法

統計学用語辞典

複数の検定結果を統合する手法(1)

　複数の検定結果を統合する手法(1)　　　Stouffer-method (Rosenthal, 1984)
　対象とする研究は「片側検定」である。

1. 個々の検定結果の P 値(pi) を Z 値(zi) に変換する
   　　　
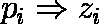
   逆の結論を与えた研究の P 値を変換するときには注意（求められた Z 値の符号を逆にする）
   
2. Z 値の合計を検定の個数(k)の平方根で割ったもの Zoverall は正規分布に従う
   　　　
   
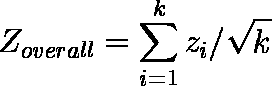
3. Zoverall から，統合された P 値 poverall を求める
   　　　

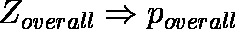
　これを AWK スクリプトで書いてみると以下のようになる。

---------- begin
# 独立な検定結果の統合
# このスクリプトには，pxg.awk，gxp.awk が必要

BEGIN {
    k = z = 0
    while ((getline p) > 0) {
        printf "%g", p
        z = pxg(p < 0 ? 1+p : p)
        if (p < 0) z = -z
        printf " %gn", z
        z_o += z
        k++
    }
    z_o /= sqrt(k)
    print "z(overall) =", z_o
    print "p(overall) =", gxp(z_o)
}
---------- end

　テストデータは，各研究で得られた P 値（片側検定）。４番目の -0.03981 は，他の研究と逆の結論を与えたもので，スクリプトの都合でそのような場合には P 値に負の符号をつけて用意する（元の 0.03981 を Z に 変換してその符号を負にすることなどと同じ意味）。

---------- begin
0.1662
0.0000023
0.04559
-0.03981
---------- end

得られる結果は，

---------- begin
pi        zi
0.1662     0.969291
2.3e-06    4.58225
0.04559    1.68921
-0.03981  -1.7529

zoverall = 2.74393
poverall = 0.00303546
---------- end

　poverall を見ることで，４つの研究成果をまとめて，「有意差あり」という結論を得る。
　さらに，「どの程度の有意な差であるか」を検討する必要がある。


参考文献

1. Rosental, R. (1984). Meta-analytic procedures for social research.
   Beverly Hills, CA:Sage.

複数の検定結果を統合する手法(2)

　複数の検定結果を統合する手法(2)　　　Stouffer-method (Rosenthal, 1984)
　対象とする研究は「片側検定」である。
　meta-analysis では，結果のちらばり(variation)を検討しなくてはならない。

1. データの一様性についての検討
   　　　
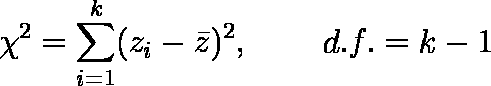
   系統的な source of variation の有無を検討しなくてはならない
   
2. effect size r を推定する
   　　　
   N は各研究におけるサンプルサイズの合計
   
3. file draw problem を検討する
   reporting bias とか publication bias と呼ばれる，「有意な結果が得られなかった場合には公表されない」ことを考慮しなくてはならない。検定結果の統合により得られた P 値 poverall が有意でなくなるためには，「有意ではない（あるいは逆の結果を与える）研究が後いくつあればよいか」という推定値(N fs.05)を計算することができる
   　　　

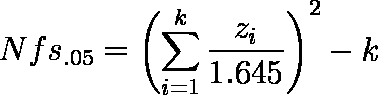
　これを AWK スクリプトで書いてみると以下のようになる。

---------- begin
# 独立な検定結果の統合-2
# このスクリプトには，pxg.awk，gxp.awk, xxp.awk が必要

BEGIN {
    k = sum_z = N = 0
    while (getline > 0) {
        p = $1
        n = $2
        z = pxg(p < 0 ? 1+p : p)
        if (p < 0) z = -z
        sum_z += z
        sz[k++] = z
        N += n
    }
    mean_z = sum_z / k
    for (i = 0; i < k; i++) {
        chi_sq += (sz[i]-mean_z)^2
    }
    print ""
    z_o = sum_z / sqrt(k)
    print "z(overall) =", z_o
    print "p(overall) =", gxp(z_o)

    print ""
    print "データの一様性の検定"
    print " カイ二乗値 =", chi_sq
    print " 自由度 =", k-1
    print " P 値 =", xxp(chi_sq, k-1)

    print ""
    print "effect size r =", z_o/sqrt(N)

    print ""
    print "N fs.05 =", (sum_z/1.645)^2-k
}
---------- end

　テストデータは，各研究で得られた P 値（片側検定）および，各研究の標本サイズ。４番目の -0.03981 は，他の研究と逆の結論を与えたもので，スクリプトの都合でそのような場合には P 値に負の符号をつけて用意する（元の 0.03981 を Z に 変換してその符号を負にすることなどと同じ意味）。標本サイズは二群の比較のようなときはそれぞれの標本サイズの合計。

---------- begin
0.1662     15
0.0000023  60
0.04559    60
-0.03981   60
---------- end

　得られる結果は，

---------- begin
zoverall = 2.74393
poverall = 0.00303546

データの一様性の検定
 カイ二乗値 = 20.3335
 自由度 = 3
 P 値 = 0.000144763

effect size r = 0.196497

N fs.05 = 7.12943
---------- end

　追加された meta-analysis により，以下の三つの所見が得られる。

1. 4 つの研究結果は，「一様ではない」ことがわかる（P 値 = 0.000144763）。
   
2. effect size r は，あまり大きなものではないことがわかる（r = 0.196497）。
   
3. poverall = 0.00303546 であったが，「有意差なし」という研究が後 ７ 編報告されると，統合した結果は有意水準 5% のもとで有意ではなくなる（N fs.05 = 7.12943）。