たじげんしゃくど‐こうせいほう〔‐コウセイハフ〕【多次元尺度構成法】
多次元尺度構成法
【英】：multidimensional scaling
概要
いくつかの対象に対して, 2対象間の距離または類似度などが与えられているとき, 多次元の空間における対象の配置を決定する方法. 各対象の座標から計算される2対象間の距離が与えられた距離にできるだけ適合するように, 配置を定める. 距離の代わりに, 複数の評定者による2対象間の選好結果, すなわち, 2対象のどちらを好むかが与えられていることもある. このときは, 対象の配置だけでなく, 評定者の理想点の位置も求められる.
詳説
マーケティングにおける製品のように, 分析の対象がいくつか考えられているときに, 2対象間の距離または類似度などから, 多次元の空間における対象の配置を決定する方法を多次元尺度構成法MDSといい, 対象の配置を布置configurationという.
対象の数を 
, 対象 
と対象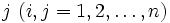 
の間の実測距離を 
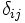とする. 類似度が得られているときは, 類似度が大きいほど距離が小さくなるように, 類似度から距離を定める. 次元の数を 
とすると, 求めるものは, 対象 
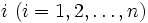の座標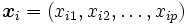 
である. 対象の布置は, 視覚的にわかりやすく表示する必要があるので, には, 2, 3のような小さい値を選ぶ.
各点の座標が定まる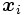と, 
と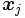 
から, たとえば, ユークリッド距離により, 対象 と対象 
の間の距離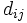 
を計算することができる. このとき, 
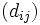は,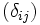 
に全体的に適合
している方がよい. そこで, 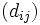が 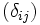に適合している程度を表す適合度を定めて, それを最小にする 
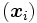を求める.
適合度の定義は, いくつか考えられているが, 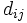と 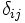の差を用いて表すものや, その差が意味を持たない場合に, 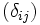と大きさに関してほぼ同じ順序を持っている距離 
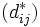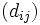を求め, と 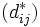の差を用いるものもある [3]. 適合度を最小にする 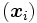を求めるのは, 非線形計画問題になる. 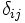が順位で与えられているときに, 相関係数の形に似た単調性係数を用いるものもある.
次元の数が定まっていないときは, の値を1から出発して, 1ずつ増やしていく方法もある. が大きくなるほど, 適合度は小さくなるが, 対象の布置はわかりにくくなる. したがって, 適合度の減少分がある限度以下になれば, 終了する.
2対象間の距離の代わりに, 複数の評定者による2対象間の選好結果が与えられていることもある. 選好結果は, 各評定者毎に, 2対象のどちらをより好むかを示す. このときは, 選考結果の集計から, 2対象の距離を計算して, 対象の布置を求めることができるだけでなく, 評定者の理想点の位置も求められる [4]. 選考判断は, 全対象に対する好みの順序で与えられることもある.
これらの他にも, 線形計画法で分析する方法 [5] や, 対象毎に, それから近い順に他の対象を並べるときの順位を求めて, それから解析する方法 [5] など, 様々な方法が提案されている.
また, 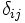を確率変数の実現値とみなす確率モデルを規定して, 最尤法などで 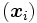を推定する方法もある [6] .
[1] 斎藤堯幸, 『多次元尺度構成法』, 朝倉書店, 1980.
[2] 高根芳雄, 『多次元尺度法』, 東京大学出版会, 1980.
[3] J. B. Kruskal, "Multidimensional Scaling by Optimizing Goodness of Fit to a Nonmetric Hypothesis," Psychometrika, 29 (1964), 1-27.
[4] J. D. Carroll, "Individual Differences and Multidimensional Scaling," in Multidimensional Scaling : Theory and Applications in the Behavioral Sciences Vol. 1, R. N. Shepard, et al. eds., New York : Seminar Press, 105-155, 1972. 岡太彬訓, 渡邊惠子 訳, 『多次元尺度構成法I理論編』, 共立出版, 1976.
[5] V. Srinivasan and A. D. Shocker, "Linear Programming Techniques for Multidimensional Analysis of Preferences," Psychometrika, 38 (1973), 337-369.
- たじげんしゃくどこうせいほうのページへのリンク
