配列
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/04/12 06:05 UTC 版)
 | この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。(2017年9月) |
 | この記事は中立的な観点に基づく疑問が提出されているか、議論中です。(2018年11月) |
この記事では、コンピュータ・プログラムにおいて配列(はいれつ、英: array)と呼ばれているデータ構造およびデータ型について説明する。計算科学方面ではベクトルという場合もある。また、リストも参照。一般に、添え字で個々の要素を区別する。
配列とは
複数の要素(値)の集合を格納・管理するのに用いられるデータ構造が配列である。数学のベクトルおよび行列に近い概念であり、実際にベクトルおよび行列をプログラム上で表現する場合に配列が使われることが多い。同様に複数要素の集合を管理するデータ構造(コレクションあるいはコンテナ)には連結リストやハッシュテーブルなどがあるが、通常はメモリアドレス上での連続性の違いなどから配列とは区別される。1次元の配列は特に線形配列 (linear array) とも呼ばれる。
例えば、6人の生徒の平均点を計算するプログラムを書くとする。配列を使わない方法では、それぞれの生徒に対応する変数を、次のように個別に用意することだろう。
int score1;
int score2;
int score3;
int score4;
int score5;
int score6;
// 例えば標準入力経由で各生徒の得点を各変数に読み込んだとする。
double mean = (double)(score1 + score2 + score3 + score4 + score5 + score6) / 6;
しかし、この方法では生徒数が増減したときに、変更や拡張が大変になってしまう。より良い解は6要素の配列を使うことである。
int score[6]; // 6要素の配列が作られる。
// 例えば標準入力経由で各生徒の得点を配列scoreに読み込んだとする。
double mean = 0;
for (int i = 0; i < 6; ++i) {
mean += score[i]; // 配列の各要素へは、変数scoreを通してscore[0]からscore[5]のようにしてアクセスする。
}
mean /= 6;
配列を用いることで、添え字演算子による統一的なアクセスおよび一括処理が可能となる。また、処理すべきデータ個数が増減したときにも対応しやすくなる。
配列の動的確保
前述の例では、プログラム中で宣言時に指定した固定のサイズ(整数定数)による配列確保(静的確保)であった。実用的には、配列の要素数が宣言時(あるいはコンパイル時)に静的に決まってしまうよりも、実行時に要素数を動的に指定して配列を確保できたほうが便利なことがある。例えば、縦横任意サイズの画像ファイルから全画素情報を読み出す場合や、コンピュータで利用可能な空きメモリ量に合わせて扱うデータ個数上限を変化させたい場合などである。
多くのプログラミング言語では、配列のサイズをプログラム実行時に指定して配列を生成する(動的に確保する)手段が用意されている。例えばC言語ではmalloc関数やcalloc関数を利用する。確保に成功するとメモリブロック(配列先頭要素)へのポインタが返却され、このポインタ経由で配列を操作する。
int numStudents;
// 例えば標準入力経由でnumStudentsに生徒数 (> 0) を読み込んだとする。
int* score = calloc(numStudents, sizeof(int)); // 要素数がnumStudents、各要素のサイズがint型のサイズであるような配列を動的に確保し、0で初期化する。
// 例えば標準入力経由で各生徒の得点を配列scoreに読み込んだとする。
double mean = 0;
for (int i = 0; i < numStudents; ++i) {
mean += score[i]; // 動的に確保した場合でも、配列の添え字シンタックスは同じ。
}
mean /= numStudents;
free(score); // 使い終わった配列のメモリ領域を解放する。
C++などの後発の言語では、動的メモリ確保のために通例new演算子が用意されていることが多く、配列の動的確保には型と要素数を指定するnew[]演算子を使用する。
int numStudents;
// 例えば標準入力経由でnumStudentsに生徒数 (> 0) を読み込んだとする。
int* score = new int[numStudents](); // 要素数がnumStudentsであるようなint型の配列を動的に確保し、0で初期化する。
// 例えば標準入力経由で各生徒の得点を配列scoreに読み込んだとする。
double mean = 0;
for (int i = 0; i < numStudents; ++i) {
mean += score[i]; // 動的に確保した場合でも、配列の添え字シンタックスは同じ。
}
mean /= numStudents;
delete[] score; // 使い終わった配列のメモリ領域を解放する。
いずれにせよ、C/C++ではmallocあるいはnewによってヒープ領域から確保したメモリは明示的に解放する必要があり、解放を忘れるとメモリリークの原因となる。プログラミングの煩雑さを解消するため、C++ではコンストラクタ・デストラクタを使ったメモリ寿命管理手法 (RAII) が使われることが多い。Javaなどの後発の言語ではガベージコレクションによる自動解放を導入していることが多く、また配列の確保に関して静的確保・動的確保といった区別をしない(配列の確保はすべて動的確保である)ことが多い。
通例、上記のようにして「動的に確保された配列」は、後述の「動的配列」とは異なり、要素の追加時に自動的にサイズを増加させるようなことはできない。
なお、C言語には後述する可変長配列も言語機能として備わっているが、メモリの生存期間などの面で違いがある。
計算オーダー
「配列」という語は、抽象データ型というよりも、添え字をオフセットとしてメモリのアドレスにマップすることで、Ο(1) でアクセスできる具象あるいは実装を特に指す場合がある(その意味では、次節の連想配列などは「配列」ではない、ということになる)。
配列に要素を挿入/削除する際、要素間に「隙間」が無いようにするには、線形リストと異なり、挿入/削除位置から後ろの領域にあるすべてのデータの移動(コピー)が必要となる。そのため、挿入/削除にO(n)時間かかる。さらに配列は連続領域を必要とするため、挿入時に領域が不足した場合に拡張する際のメモリ再確保のコストが高い。
探索は一般的には線型探索になるためΟ(n)だが、データがソート済みであれば二分探索を使うことでΟ(log n)に軽減することもできる(抽象データ型としては、sorted array などの名前で別のデータ構造と考える場合もある。en:Sorted array を参照)。
さまざまな配列
連想配列
添え字は一般に通例0か1始まりの (非負) 整数である。一方、文字列など他のデータ型を添え字のように使用できる配列を連想配列という。
固定長配列
決まった要素数しか格納できない配列を、固定長配列 (fixed-length array, fixed-size array) あるいは静的配列 (static array) と呼ぶ。
動的配列
要素数によって自動的にサイズが拡張される配列を、動的配列 (dynamic array, growable array, resizable array) と呼ぶ。メモリが許す限り、要素の末尾追加や途中挿入がいくらでもできる。標準ライブラリで提供されるもの(C++のstd::vector[1]、Javaのjava.util.ArrayList[2]、.NETのSystem.Collections.Generic.List[3][注釈 1]、Pythonのlist[4]、ECMAScriptのArray[5]など)と、言語に組み込まれているもの(PerlやDなど)がある。またPerlなど、言語によっては、最初に配列を生成する際に指定されたサイズからはみ出してアクセス(範囲外アクセス)しても、自動的に拡大されるような配列を持っているものもある。
動的配列の拡大などの場合には、最悪の場合、メモリ上の別の場所が確保されて、そこに全体をコピーする、というような時間のかかる操作が起きる可能性があるものもある(そのシステムの設計次第で、配列の内部にあるものが他からポインタで指されていて、それを更新できないなど、そういうことができない場合もある)。最悪計算量ではなく償却計算量でO(1)になれば良い、という考え方もある。
可変長配列
なおC言語では、下記のように、実行時に(整数定数式ではない)要素数を指定してスタック上に自動変数として確保することのできる静的配列を可変長配列 (variable-length array) と呼んでいる[6]。GCCに拡張として実装されていたが、C99以降で標準化された。この可変長配列は後から要素を追加したりすることはできない。
void func(size_t n) {
int data[n];
}
多次元配列
1次元だけではなく2次元・3次元などの多次元配列 (multidimensional array) を備える言語もある。 マトリックスやグリッドのような矩形構造を持ったデータ構造であることから、矩形配列 (rectangular array) と呼ばれることもある[7]。
C#やFORTRANなど、一部の言語には「真の」多次元配列があり、a[i, j] などといったような構文でアクセスする。
C#による多次元配列の例を示す。
int[,] array2d = {
{0, 1, 2, 3},
{4, 5, 6, 7},
{8, 9, 10, 11},
};
System.Console.WriteLine(array2d[2, 3]);
C#には、後述するジャグ配列となる「配列の配列」もある。
C言語の場合
C言語は規格で多次元配列に関する言及があるが、実際にサポートされているのは「配列の配列」であって、真の多次元配列ではない[8]。次のようなコードのことを考えてみればわかる。
void f(int (*p_arr3)[3]) {
……
}
int main(void) {
int arr5_arr3[5][3];
f(arr5_arr3);
return 0;
}
ここで arr5_arr3 は「『intの3要素の配列』の5要素の配列」である。そして、関数fに渡される際には、C言語の「配列は引数として渡される際は、その先頭要素を指すポインタに縮退する」というルールにより、その先頭の「intの3要素の配列」を指すポインタがp_arr3に渡される。
もし仮にC言語で真の多次元配列がサポートされているならば、それぞれ「intの5x3要素の配列」「『intの5x3要素』を指すポインタ」(あるいは、単にintを指すポインタに縮退するかもしれない)などがサポートされるはずだが、実際にはサポートされない。
Javaの場合
Javaの「配列の配列」はC言語よりもさらに緩く、Javaの型システムにおける「配列の配列」では、外側の配列は、内側の配列のサイズを固定しない(C言語では、内側の配列のサイズは固定である)。さらに、Javaにはプリミティブ型と参照型があり、参照型は一種のポインタだが、配列は参照型であるので、Javaの「配列の配列」は後述の「ジャグ配列」になっており、やはり真の多次元配列がサポートされているとは言えない。もちろん、1次元配列に対し多次元配列風にアクセスする機能を提供するようなクラスを実装することはできるが、それでは言語レベルで真の多次元配列がサポートされているとは言えない。
ジャグ配列
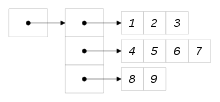
「配列の配列」の場合、内側の配列について、要素数が揃っていることを要求しないデータ構造であることもある。ジャグ配列 (jagged array)、不規則配列などと言う。これに対し、内側の配列の要素数が揃った配列を矩形配列 (rectangular array) などと言う。Javaにおける配列の配列はジャグ配列である。C#には前述の通り、「真の多次元配列」もあるが、それとは別に配列の配列もあり、そちらはJavaと同様のジャグ配列である。
Javaによるジャグ配列の例を示す。
int[][] numArr = new int[3][];
numArr[0] = new int[]{1, 2, 3};
numArr[1] = new int[]{4, 5, 6, 7};
numArr[2] = new int[]{8, 9};
System.out.println(numArr[1][1]);
C#によるジャグ配列の例を示す。
int[][] numArr = new int[3][];
numArr[0] = new int[]{1, 2, 3};
numArr[1] = new int[]{4, 5, 6, 7};
numArr[2] = new int[]{8, 9};
System.Console.WriteLine(numArr[1][1]);
要素のアドレスを指定するための参照の展開は、ジャグ配列では次元の数だけ必要なのに対し、矩形配列では1回で済む。また配列の領域を確保する際、ジャグ配列では次元ごとに領域確保を繰り返す必要があるのに対し、矩形配列では1回のnew演算子の使用で領域が確保できる。ただし矩形配列は全要素が収まる連続領域を確保しなければならず、疎行列などのまばらな配列には空間的オーバーヘッドが大きくなってしまうことから向いていない。また、.NET Frameworkの中間言語には1次元配列の要素アクセスに関する専用命令が存在するため、矩形配列よりもジャグ配列のほうが速度性能面で有利になるケースも存在する[9]。
C言語では、配列を指すポインタは、その配列のサイズを固定しなければならない。配列を指すポインタではなく、「『配列の先頭要素を指すポインタ』の配列」によって、次のようにしてジャグ配列のようなデータ構造を作ることができる。
int *numArr[3];
int tmp0[] = {1, 2, 3};
int tmp1[] = {4, 5, 6, 7};
int tmp2[] = {8, 9};
numArr[0] = tmp0;
numArr[1] = tmp1;
numArr[2] = tmp2;
printf("%d\n", numArr[1][1]); // print "5"
例示したように、「配列の配列」と同様の構文でアクセスできるが、データ構造としては異なっている[要追加記述]。当然、(生成されるコード[要追加記述]を読めばわかるが)意味的に違うものであって、混同してはならない。ましてや「多次元配列がサポートされていると考えるべき」などと考えるのは、混乱の元でしかない。
Iliffe vector
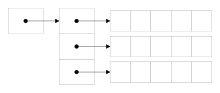
「ジャグ配列と同様な構造で実装された、多次元配列」という意味の、Iliffe vector という語がある("Iliffe" は、人名 John K. Iliffe に由来)。それに対し、連続した領域を多次元配列として扱うデータ構造を指す dope vector(en:Dope vector)という語がある。
脚注
注釈
- ^ リンクリストではなく、メモリ上で連続しているため、ランダムアクセスは定数時間のO(1)となる。
出典
- ^ “std::vector - cppreference.com”. ja.cppreference.com. 2024年4月12日閲覧。
- ^ “ArrayList (Java SE 21 & JDK 21)”. docs.oracle.com. 2024年4月12日閲覧。
- ^ dotnet-bot. “List<T> クラス (System.Collections.Generic)”. learn.microsoft.com. 2024年4月12日閲覧。
- ^ “リスト型 (list) - 組み込み型”. Python documentation. 2024年4月12日閲覧。
- ^ “Array - JavaScript”. 2024年4月12日閲覧。
- ^ ARR32-C. 可変長配列のサイズ引数は適切な範囲内にあることを保証する
- ^ 多次元配列・ジャグ配列 - Programming/.NET Framework/配列 - 総武ソフトウェア推進所
- ^ ISO/IEC 9899:1999 - n1256.pdf
- ^ 配列 - C# によるプログラミング入門 | ++C++; // 未確認飛行 C
固有名詞の分類
品詞の分類
「配列」に関係したコラム
-
FX(外国為替証拠金取引)のチャート分析ソフトMT4(Meta Trader 4)での時刻表示は、MT4のダウンロード先にもよりますが、一般的には中央ヨーロッパ時間であることが多いようです。日本時間の...
- >> 「配列」を含む用語の索引
- 配列のページへのリンク

