順列と確率
確率を求めるためには,全体の場合の数と,ある条件を満たす場合の数とを数え上げることが必要であるが,その際,順列・組合せの考え方が有用である(場合の数があまり大きくないときには,全ての場合を,漏れなく重複なく列挙するのが有効であり,非常に大きくなったときにも,その考え方は変わらないが,順列・組合せの考え方を用いると簡単である)。
順列
n 個の異なるものから,r 個をとって 1 列に並べたものを,n 個のものから r 個をとる 順列 といい,この順列の総和を nPr で表す。
nPr = n ( n - 1 ) ( n - 2 ) … ( n - r + 1 )
特に,nPn = n ( n - 1 ) ( n - 2 ) … 3 ・ 2 ・ 1 は 1 から n までの自然数の積であり,n ! で表し,n の 階乗 という。この記法を用いると,
nPr = n ! / ( n - r ) !
となる( 0 ! = 1 と定義する )。
例題:
0,1,2, … ,9 の数字を書いた 10 枚のカードをよく切り,ランダムに 4 枚を抜き出して順に 1 列に並べる。このときできる整数が 7000 以上になる確率を求めよ。
解答:
- 1 番目の場所には,10 枚のカードのどれを入れてもよいから 10 通りの入れかたがある。
- 次にその各々の入れかたに対して,2 番目の場所には 1 番目に入れたものを除く 9 枚のどれを入れてもよいから 9 通りの入れかたがある。
- 同様にして,3 番目の場所には 8 通り,4 番目の場所には 7 通りの入れかたがある。
- したがって,できる整数は 10P4 = 10 × 9 × 8 × 7 = 5040 通りあることがわかる。
- 7000 以上の整数ができるためには,千の位にくるカードが 7,8,9 のいずれかであることが必要であり,そうであれば十分である。したがって,千の位には 3 通りの入れかたがある。
- 次に,その各々の入れかたに対して,百,十,一の位への入れかたは,千の位に入れた 1 枚を除く 9 枚から 3 枚をとる順列を考えればよい。
- したがって,条件を満たす整数の個数は,3 × 9P3 = 3×9×8×7 = 1512 個である。
- 各順列は全て同様の確からしさで起こるから,求める確率は
3 × 9P3 / 10P4 = 3 / 10 = 0.3
である。
重複順列
n 個の異なる種類のものから,繰り返しを許して r 個をとるとき,得られる順列を,n 個のものから r 個をとる 重複順列 といい,その数は nr に等しく,nΠr で表す。
例題:
0,1,2, … ,9 の数字を書いた 10 枚のカードをよく切り,ランダムに 1 枚を抜き出す。カードをもとに戻し,よく切ってからもう一度ランダムに 1 枚を抜き出す。このような手順を 4 回繰り返して,引いたカードの数値を順に 1 列に並べる。このときできる整数が 7000 以上になる確率を求めよ。
解答:
- 1 番目の場所には 10 通りの入れかたがある。
- その各々に対して 2 番目の場所にも 10 通りの入れかたがある。
- 同様に,3,4 番目の場所にも 10 通りの入れかたがある。すなわち,10Π4 = 104 = 10000 通りの可能性がある。
- 次に,7000 以上の整数が得られるのは,千の位に 7,8,9 が来るときで,その各々の入れかたに対して,百,十,一の位への入れかたは 10Π3 = 103 通りある。
- したがって,条件を満たす整数の個数は,3 × 10Π3 = 3×103 = 3000 個である。
- 各順列は全て同様の確からしさで起こるから,求める確率は
3 × 10Π3 / 10Π4 = 3 / 10 = 0.3
である。
組合せ
n 個の異なるものから,r 個をとってできる組を,n 個のものから r 個をとる 組合せ といい,この総数を nCr で表す。
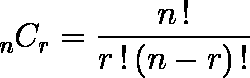
となり,nC0 = 1 となることもわかる。
例題:
52 人のクラスで,うち 17 人は女子である。このクラスで,くじ引きによって 4 人の委員を選ぶとき,4 人とも女子になる確率を求めよ。
解答:
- 52 人から 4 人を選ぶ選び方は 52C4 通りある。
- 4 人の委員が全員女子である組み合わせは 17C4 通りある。
- 各組あわせは同様の確からしさで起こるから,求める確率は 17C4 / 52C4 = 0.0087912 である。
重複組合せ
n 個の異なるものから,繰り返しを許して r 個をとってできる組合せを,n 個のものから r 個をとる 重複組合せ といい,この総数を nHr で表す。
nHr = n + r - 1Cr
順列と確率と同じ種類の言葉
- 順列と確率のページへのリンク
