母比率の信頼区間
例題：
「内閣の支持率を 500 人の有権者に調査したところ 35% であった。支持率の 95% 信頼区間を求めなさい。」
推定手順：
- 記号の定義
ケース数を n，そのうちで対象とする属性を持つもの（陽性数と呼ぶことにする）の数を r とする。標本比率を p，信頼率を A とする。
例題では，n = 500，p = 0.35，r = n p = 175，A = 0.95 である。
- (1-α) 100 % 信頼限界を求める。信頼率に対応する α を求めておく（α = (1-A)）。
例題では，α = 0.05 である。
- 条件により以下の方法をとる。
- p = 0 の場合
上側信頼限界 = 1-α1/n
多くの統計パッケージでは 1-(α/2)1/n と定義してある（主義の違い）
下側信頼限界 = 0
- p =1 の場合
下側信頼限界 = α1/n
多くの統計パッケージでは (α/2)1/n と定義してある（主義の違い）
上側信頼限界 = 1
- 0 ＜ p ＜ 1 の場合
- 正規分布により近似する方法
標準正規分布において上側確率が α/2 となる値を Z とする。
正規分布表，または 正規分布のパーセント点の計算を参照すること。
信頼限界は次式で与えられる。
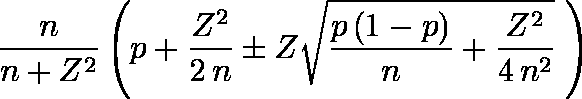
注：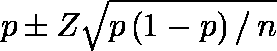
という式（Waldによる）が用いられることが多いが，ケース数(n)が小さいときには用いないほうがよいであろう。
Agresti と Coull が提唱した修正法はかなり良い信頼区間を与えるようである。
例題では，Z = 1.96 であり，下側信頼限界 = 0.30948，上側信頼限界 = 0.39281 となる。
- F 分布に基づく方法
ν1 = 2（n-r+1），ν2 = 2 r を自由度とするF 分布で，上側確率が α/2 となる値を F とする。
ν1'= 2（r+1），ν2'= 2（n-r）を自由度とする F 分布で，上側確率が α/2 となる値を F'とする。
F 分布表（α = 0.05，α = 0.025，α = 0.01，α = 0.005），または F 分布のパーセント点の計算を参照すること。
下側信頼限界 =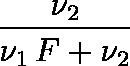
上側信頼限界 =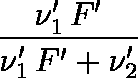
例題では，n = 500, p = 0.35 より，r = 175 であり，
ν1 = 652，ν2 = 350 となり，F = 1.20502
ν1'= 352，ν2'= 650 となり，F'= 1.19857
となる。これにより，
下側信頼限界 = 350/(652・1.20502+350) = 0.30819
上側信頼限界 = 352・1.19857 / (352・1.19857 + 650) = 0.39360
となる。
- 正規分布により近似する方法
- p = 0 の場合
補足説明
- F 分布による検定において，母比率が 0.5 でないときは，分布が歪んでいるので両側検定の結果は注意して用いなければならない。
正確には，F 分布に基づいて信頼区間を求め，信頼区間に母比率が含まれる場合に帰無仮説を採択し，含まれない場合に帰無仮説を棄却するという手続きをとった方がよい（この考え方は，分布が歪んでいるときに下側確率と上側確率を別々に求めることを意味しており，これにより正確な有意確率を求めることができる）。 - 標本比率が 0 であっても，上側信頼限界は 0 ではない。同じように，標本比率が 1 であっても，下側信頼限界は 1 ではない。
- 母比率の信頼区間のページへのリンク
