積分幾何学
【英】:integral geometry
概要
"ビュッフォンの針"のように図形に関係した確率を幾何確率といい, これらの理論的な部分は, 積分幾何学を基礎にしている. 積分幾何学の基礎概念とは合同変換によって不変な測度(積分)を求めることにあり, 対象が点, 直線, 一般的な図形等でそれらの集合の不変な測度がそれぞれ得られる. その測度(積分)に関係して, 直線についてはクロフトン (Crofton) による, 一般的な図形についてはブラシュケ (Blaschke) による, きれいな主公式が存在する.
詳説
“ビュッフォンの針”のように図形に関係した確率を幾何確率といい, これらの理論的な部分は, 積分幾何学(integral geometry)を基礎にしている. 積分幾何学は幾何確率に応用可能であるばかりでなく, もっと広く図形に関する様々な局面で基礎となり得ると考えられる. そこで積分幾何学の基礎概念と直線に関する主公式にかぎって述べることにする. 詳しくは[1], [2]を参照されたい. 積分幾何学の基礎概念とは合同変換によって不変な測度を求めることにあるが, 例を直観では分かりづらい直線の集合に採り, 以下で議論を展開する.
図1のように, 直線 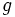 があって, 原点からこれに下ろした垂線の長さを
があって, 原点からこれに下ろした垂線の長さを  , 垂線と
, 垂線と  軸との角度を
軸との角度を 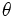 とすると, この直線は
とすると, この直線は
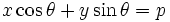
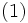
と表される. そこで, この と
と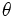 で, 直線の集合(たとえばある領域と交わる直線の集合など)の測度を
で, 直線の集合(たとえばある領域と交わる直線の集合など)の測度を

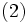
とおき, 以下, 合同変換で不変の条件を考えよう. 直線 (1)で表されるような, 直線の集合  が,
が,
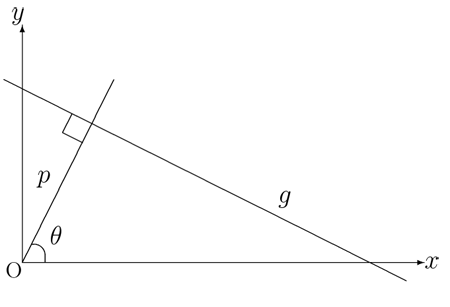 |
| 図1:直線に下ろした垂線 |
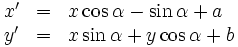
によって,
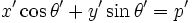
なる直線の集合 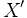 に変換されたものとする. すると, 上式より
に変換されたものとする. すると, 上式より
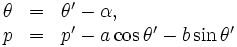
が得られる. ここで, 一様な直線の分布を考えているので,  と
と 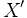 の測度は等しく, すなわ
ち
の測度は等しく, すなわ
ち
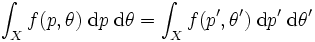
でなければならない. ところが, 式 (4)から  より
より 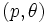 への変数変換のヤコビアンは1なので, 上式の右辺を変形して
への変数変換のヤコビアンは1なので, 上式の右辺を変形して
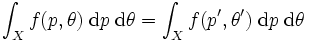
と表すことができ, これは  をどのようにとっても成立しなければならないので,
をどのようにとっても成立しなければならないので,
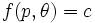
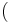 定数
定数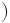
が得られる. そこで 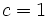 とし,
とし, 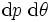 を
を 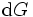 とおいて, これを直線の集合
とおいて, これを直線の集合  の密度を表わすとすれば, 直線の集合の測度が式 (2)より
の密度を表わすとすれば, 直線の集合の測度が式 (2)より
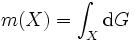
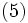
と導かれる. ここで, 図2のような滑らかな曲線ABがあり, その長さを 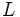 とする. AB上の点Pでこの曲線と交わる直線を
とする. AB上の点Pでこの曲線と交わる直線を 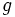 , 曲線ABのPにおける接線と
, 曲線ABのPにおける接線と 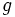 とのなす角度を
とのなす角度を 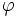 , AからPまでの曲線上の長さを
, AからPまでの曲線上の長さを 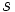 とおく. すると,
とおく. すると, 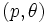 から
から 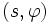 への変数変換におけるヤコビアンは
への変数変換におけるヤコビアンは 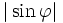 となり, 曲線ABと交わる直線のすべては,
となり, 曲線ABと交わる直線のすべては, 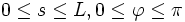 の範囲を考えればよい. ゆえに
の範囲を考えればよい. ゆえに
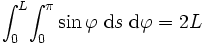
となるので, この 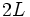 を曲線
を曲線 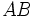 と交わる直線の集合の測度
と交わる直線の集合の測度 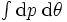 としてよいかにみえる. ところが上記の積分は曲線
としてよいかにみえる. ところが上記の積分は曲線 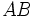 に沿って行なわれたので, この曲線と二つ以上の点で交わる直線については, それぞれの交点で計算されている. したがって, 上記の
に沿って行なわれたので, この曲線と二つ以上の点で交わる直線については, それぞれの交点で計算されている. したがって, 上記の 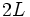 という値は求めたい測度よりも大きい数値であり,
という値は求めたい測度よりも大きい数値であり, 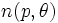 でこの重複を表現すれば
でこの重複を表現すれば
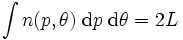
が得られる. ところで, 曲線ABを滑らかなものとして議論してきたが, 滑らかな曲線を有限個つなげたものや, 不連続なものについても, ほとんどいたるところで接線は存在するので, 上式は成立する. そして対象となる曲線と交わらない直線については, 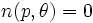 と解釈し,
と解釈し,
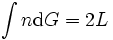
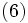
が導かれる. さて, これをもとに, 簡単な図形と交わる直線の集合の測度を求めよう. まず上記の曲線ABが直線分であれば, ほとんどいたるところ 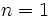 なので, 長さ
なので, 長さ 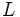 の線分と交わる直線の集合
の線分と交わる直線の集合  の測度は
の測度は
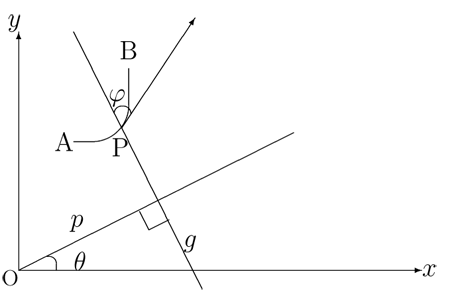 |
| 図2:曲線と直線 |
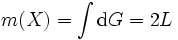
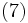
となる. 次に曲線が凸閉曲線の場合, ほとんどいたるところ 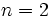 が成立するので, 長さ
が成立するので, 長さ 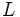 の凸閉曲線と交わる直線の集合
の凸閉曲線と交わる直線の集合  の測度は
の測度は
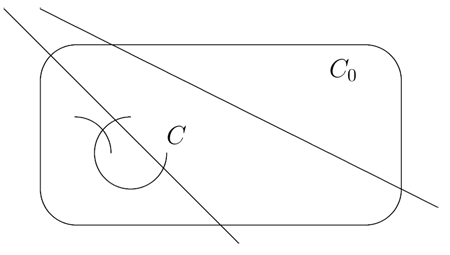 |
図3: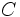 と交わる確率 と交わる確率 |
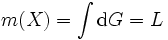
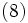
となる. これを用いると, 以下のような確率を簡単に求めることができる. 図3のように凸閉曲線 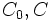 があって, 長さをそれぞれ,
があって, 長さをそれぞれ, 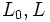 とする. 曲線
とする. 曲線 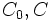 に交わる直線の集合を
に交わる直線の集合を 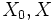 とすれば,
とすれば, 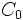 に交わる直線が,
に交わる直線が, 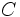 にも交わる確率
にも交わる確率  は, 式(8)より
は, 式(8)より
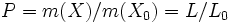
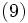
となる.
[1] L.A.Santaló, Integral Geometry and Geometric Probability, Addison-Wesley, Reading, Massachusetts, 1976.
[2] 腰塚武志, 「積分幾何学について(1)~(4)」, 『オペレーションズ・リサーチ』, 21 (1976), 524-529, 591-596, 654-659, 711-717.
積分幾何学と同じ種類の言葉
- 積分幾何学のページへのリンク
