ポアソン‐ぶんぷ【ポアソン分布】
ポアソン分布
ポアソン分布
ポアソン分布 の確率関数は次式で表される。
 ……(1)
……(1)ただし,x = 0,1, … , λ > 0
ポアソン分布の概形は図 1 のようになるが,λが大きくなると正規分布に近づく(アニメーション,または,ムービー)。
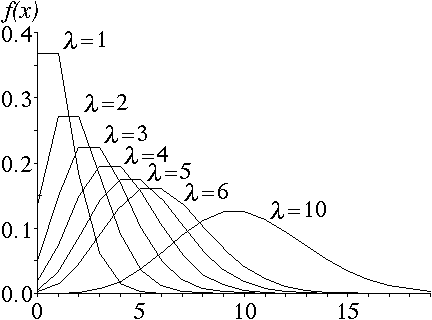 図 1.ポアソン分布の概形 |
|---|
二項分布において,生起確率 p が極めて小さい場合がある。このとき,n が十分に大きくても n p は有限なものとなる。そこで,n p = λ とおき,n → ∞,p → 0 としたとき,二項分布の( 1 )式の確率関数 f ( x ) を,λ と x を用いて表すことを考える。
p = λ / n を二項分布の( 1 )式に代入すると,次式のようになる。

ここで,

および

に注意すると,( 1 )式になる。
ポアソン分布の平均 E ( x ) ,分散 V ( x ) は二項分布との関係より,
E ( x ) = V ( x ) = λ
である。
例題: 「自動車事故による死亡が 1 年間に 1 万人であるとする。日本の人口を 11,600 万人,ある都市の人口を 100 万人としたとき,その都市で自動車事故による死亡が一件もないという日が起こる確率を求めよ。」
解答: ある一人の人が交通事故にあう 1 日あたりの確率 p はきわめて小さい。
p = 10000 / ( 116000000・ 365 ) = 2.362 × 10 - 7
また,この都市の人口はきわめて大きいので,交通事故死の確率はポアソン分布に従うと考えられる。
ポアソン分布のパラメータ λ は,
λ = n p = 1000000・ 2.362 × 10 - 7 = 0.2362
となる。
( 1 )式より,求める確率は f ( 0 ) = 0.790 となる。
このほか,ポアソン分布に当てはまる事象としては,製品中の不良品の個数,一定時間内に電話がかかってくる回数などがあげられる。
ポアソン分布
| 確率と確率過程: | ファイナンシャルエンジニアリング ブラウン運動 ブロックガウス・ザイデル法 ポアソン分布 ポアソン過程 マルコフ型到着過程 マルコフ変調ポアソン過程 |
ポアソン分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/12/23 07:01 UTC 版)
統計学および確率論で用いられるポアソン分布(英: Poisson distribution)とは、ある事象が一定の時間内に発生する回数を表す離散確率分布である。
- ^ @teramonagi (2012年1月28日). “指数分布とポアソン分布のいけない関係”. SlideShare. 2012年1月27日閲覧。
- ^ 土居正明. 二項分布と Poisson 分布の平均・分散 (PDF) (Report). ポアソン分布の平均と分散の導出
- ^ “Do bacterial cell numbers follow a theoretical Poisson distribution? Comparison of experimentally obtained numbers of single cells with random number generation via computer simulation” (英語). Food Microbiology 60: 49–53. (2016-12-01). doi:10.1016/j.fm.2016.05.019. ISSN 0740-0020.
- ^ Ladislaus von Bortkiewicz (1898) (PDF), Das Gesetz der kleinen Zahlen, University of Wasington Library, Leipzig Druck und Verlag von B.G.Teubner 復刻版が2010年にNabu Pressより発売されている
- ^ Par Simeon Denis Poisson (1857) (PDF), Recherches sur la probabilité des Jugements, Des Regles Generares du Calcul des Probabilites, Bacheliar, Impremeur-Libraire.
ポアソン分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/02/07 05:36 UTC 版)
隣接する固有値が区間[λ+S,λ+S+dS]に見つかる確率P(S)dSが固有値の値λや間隔 S とは相関がなく独立している(つまり定数)と仮定すると、固有値の最近接間隔分布はポアソン過程において連続して起こる事象の生起間隔の分布と同じ指数分布になる。 P ( s ) ∼ e − s {\displaystyle P(s)\sim e^{-s}}
※この「ポアソン分布」の解説は、「ランダム行列」の解説の一部です。
「ポアソン分布」を含む「ランダム行列」の記事については、「ランダム行列」の概要を参照ください。
ポアソン分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/11/09 06:39 UTC 版)
「モーメント (確率論)」の記事における「ポアソン分布」の解説
確率質量関数が P ( x = k ) = λ k e − λ k ! {\displaystyle P(x=k)={\frac {\lambda ^{k}e^{-\lambda }}{k!}}} で与えられるポアソン分布において、モーメントは次のように与えられる。 m 1 = λ m 2 = λ 2 + λ m 3 = λ 3 + 3 λ 2 + λ ⋮ {\displaystyle {\begin{aligned}m_{1}&=\lambda \\m_{2}&=\lambda ^{2}+\lambda \\m_{3}&=\lambda ^{3}+3\lambda ^{2}+\lambda \\&\vdots \end{aligned}}}
※この「ポアソン分布」の解説は、「モーメント (確率論)」の解説の一部です。
「ポアソン分布」を含む「モーメント (確率論)」の記事については、「モーメント (確率論)」の概要を参照ください。
ポアソン分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2020/09/10 03:22 UTC 版)
n が大きく p が十分小さい場合、np は適度な大きさとなるため、λ = np を母数とするポアソン分布が二項分布 B(n, p) の良好な近似を与える。すなわち、n が十分大きいとき、期待値 λ = np とおくと、 P [ X = k ] ≃ λ k e − λ k ! {\displaystyle P[X=k]\simeq {\frac {\lambda ^{k}e^{-\lambda }}{k!}}} が成り立つ(詳細はポアソン分布の項を参照)。この結果は数学者シメオン・ドニ・ポアソンが1837年に著書 Recherches sur la probabilite des jugements (Researches on the Probabilities) の中で与えており、ポアソンの極限定理と呼ばれる。
※この「ポアソン分布」の解説は、「二項分布」の解説の一部です。
「ポアソン分布」を含む「二項分布」の記事については、「二項分布」の概要を参照ください。
ポアソン分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/11/13 22:25 UTC 版)
確率分布関数が P ( x = k ) = λ k e − λ k ! {\displaystyle P(x=k)={\frac {\lambda ^{k}e^{-\lambda }}{k!}}\,} で与えられるポアソン分布において、キュムラント母関数は次のように与えられる。 log M ( s ) = λ ( e s − 1 ) = ∑ n = 1 ∞ λ s n n ! {\displaystyle \log {M(s)}=\lambda (e^{s}-1)=\sum _{n=1}^{\infty }{\frac {\lambda s^{n}}{n!}}} 従って、全てのキュムラント cn は λ となる。 c n = λ n = 1 , 2 , … {\displaystyle c_{n}=\lambda \quad n=1,2,\dots }
※この「ポアソン分布」の解説は、「キュムラント」の解説の一部です。
「ポアソン分布」を含む「キュムラント」の記事については、「キュムラント」の概要を参照ください。
ポアソン分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/09/16 01:21 UTC 版)
X1, ...., Xn を、母数λ のポアソン分布に従う独立な確率変数とする。和 T(X) = X1 + ... + Xn が λ に対する十分統計量である。同時確率は: Pr ( X = x ) = P ( X 1 = x 1 , X 2 = x 2 , … , X n = x n ) . {\displaystyle \Pr(X=x)=P(X_{1}=x_{1},X_{2}=x_{2},\ldots ,X_{n}=x_{n}).} 観察は独立であるから、次のように書き換えられる: e − λ λ x 1 x 1 ! ⋅ e − λ λ x 2 x 2 ! ⋅ ⋯ ⋅ e − λ λ x n x n ! {\displaystyle {e^{-\lambda }\lambda ^{x_{1}} \over x_{1}!}\cdot {e^{-\lambda }\lambda ^{x_{2}} \over x_{2}!}\cdot \,\cdots \,\cdot {e^{-\lambda }\lambda ^{x_{n}} \over x_{n}!}\,\!} さらに e − n λ λ ( x 1 + x 2 + ⋯ + x n ) ⋅ 1 x 1 ! x 2 ! ⋯ x n ! = e − n λ λ T ( x ) ⋅ 1 x 1 ! x 2 ! ⋯ x n ! {\displaystyle e^{-n\lambda }\lambda ^{(x_{1}+x_{2}+\cdots +x_{n})}\cdot {1 \over x_{1}!x_{2}!\cdots x_{n}!}=e^{-n\lambda }\lambda ^{T(x)}\cdot {1 \over x_{1}!x_{2}!\cdots x_{n}!}\,\!} これから因子分解条件が成り立ち、h(x) は全変数の階乗の積の逆数である。
※この「ポアソン分布」の解説は、「十分統計量」の解説の一部です。
「ポアソン分布」を含む「十分統計量」の記事については、「十分統計量」の概要を参照ください。
ポアソン分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/11/18 11:23 UTC 版)
「ジェフリーズ事前分布」の記事における「ポアソン分布」の解説
非負の整数 n {\displaystyle n} についてのポアソン分布の場合を考える: f ( n ∣ λ ) = e − λ λ n n ! , {\displaystyle f(n\mid \lambda )=e^{-\lambda }{\frac {\lambda ^{n}}{n!}},} レートパラメータ λ ≥ 0 {\displaystyle \lambda \geq 0} についてのジェフリーズ事前分布は p ( λ ) ∝ I ( λ ) = E [ ( d d λ log f ( n ∣ λ ) ) 2 ] = E [ ( n − λ λ ) 2 ] = ∑ n = 0 + ∞ f ( n ∣ λ ) ( n − λ λ ) 2 = 1 λ . {\displaystyle {\begin{aligned}p(\lambda )&\propto {\sqrt {I(\lambda )}}={\sqrt {\operatorname {E} \!\left[\left({\frac {d}{d\lambda }}\log f(n\mid \lambda )\right)^{2}\right]}}={\sqrt {\operatorname {E} \!\left[\left({\frac {n-\lambda }{\lambda }}\right)^{2}\right]}}\\&={\sqrt {\sum _{n=0}^{+\infty }f(n\mid \lambda )\left({\frac {n-\lambda }{\lambda }}\right)^{2}}}={\sqrt {\frac {1}{\lambda }}}.\end{aligned}}} 同等に、 λ = ∫ d λ / λ {\textstyle {\sqrt {\lambda }}=\int d\lambda /{\sqrt {\lambda }}} についてのジェフリーズ事前分布は、非負の実数直線上の正規化されていない一様分布である。
※この「ポアソン分布」の解説は、「ジェフリーズ事前分布」の解説の一部です。
「ポアソン分布」を含む「ジェフリーズ事前分布」の記事については、「ジェフリーズ事前分布」の概要を参照ください。
ポアソン分布と同じ種類の言葉
- ポアソン分布のページへのリンク
 をとる
をとる を
を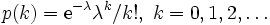 で
で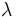 である.
である.