非一様乱数

OR事典

非一様乱数

読み方：ひいちようらんすう
【英】：non-uniform random numbers

概要

一様分布以外の分布をする乱数の総称. 一様乱数に適当な変換を施して作るのがふつうである. 変換法として, 逆関数法, 棄却法, 合成法, 別名法, 一様乱数の比を利用する方法, 等の種々の分布に適用可能な方法と, 個々の分布に特有の方法が多数提案されている.

詳説

　一様分布以外の確率分布に従う乱数を非一様乱数という. これらの乱数は, 一様乱数に適当な変換を施して作るのがふつうである. 変換方法には, 種々の分布に対して適用可能な一般的なものと, 個々の分布の特徴を利用するものとがある. これらの方法を網羅的に扱っているのが [3]である. ここでは, 一般的な変換法を二つ紹介した後, 実用上大事な非一様乱数生成法を述べる. 以下では, (整数型の)一様乱数を正規化して得られる区間[0,1)上の(実数型の)一様乱数を等で表し, これらは互いに独立であるものと仮定する. また, 発生させたい乱数を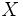とし, その分布関数を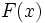, それが連続分布ならば, その密度関数を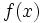で表す.

[逆関数法]

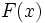　の逆関数を使ってとするものである. 例えば, 指数分布, ワイブル分布, ロジスティック分布(スケール・パラメータはいずれも1とする)なら, それぞれ, , とすればよい. 逆関数が解析的に求まらない場合には, 近似式等を用いることになる.

[二者択一法]

　ウォーカー(A. J. Walker) [4] によって提案されたもので, 別名法(alias method)ともいう.

　取りうる値の個数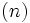が有限個の離散分布に従う乱数を, に無関係なO(1)の速度で生成できる, 簡単で効率的な方法である. ただし, 初期設定に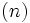Oの時間とO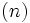のメモリを必要とする. 例えばポアソン分布のように, 取りうる値の個数が無限の場合には, 分布の裾を適当に打ち切って適用すればよい.

[正規分布]

　逆関数法を適用する場合には, 逆関数が解析的には求まらないので, 例えば次の山内二郎の近似式を使う.

ボックス・ミュラー(Box-Muller)法は, 変換公式

を使って, 2個の一様乱数から互いに独立な標準正規乱数を作るものである.

　平均ベクトルが, 分散共分散行列が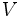の次元正規乱数ベクトルを生成するためには, 互いに独立な個の標準正規乱数からなるベクトルに変換

を施せばよい. ただし, ベクトルはすべて列ベクトルとし, 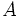は(は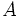の転置行列)を満たす下三角行列であり, コレスキー(Cholesky)分解によって求める.

[アーラン分布]

　フェイズが(正整数)のアーラン分布の密度関数は

である. これは, パラメータ(平均値の逆数)が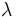の指数分布に従う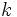個の確率変数の和の分布であるから,

とすればよい.

[ポアソン分布]

　平均値が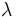のポアソン乱数は, 平均が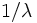の指数乱数との関係を利用して作ることができる. すなわち, が成り立つ最大の整数を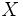とすればよい. 1個のポアソン乱数を発生するのに必要な一様乱数の個数の平均値はであるから, 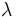が大変に大きいときには, この方法は効率が悪いので, 二者択一法を使うほうがよい.

---

参考文献

[1] 伏見正則, 『乱数』(UP応用数学選書12), 東京大学出版会, 1989.

[2] D. E. Knuth, The Art of Computer Programming, Vol.2: Seminumerical Algorithms, 2nd ed., Addison-Wesley, 1981. 渋谷政昭訳, 『準数値算法/乱数』, サイエンス社, 1981.

[3] L. Devroye, Non-Uniform Random Variate Generation, Springer-Verlag, 1986.

[4] A. J. Walker, "An Efficient Method for Generating Discrete Random Variables with General Distributions," ACM Transactions on Mathematical Software, 3 (1977), 253-256.

「OR事典」の他の用語

シミュレーション：

負相関変量法  連続型シミュレーション  連続型シミュレーション言語  重点サンプリング  離散型シミュレーション  離散型シミュレーション言語  非一様乱数