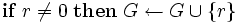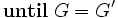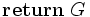グレブナー基底
【英】:Gröbner basis
概要
多変数多項式環の基底の一種で,多項式の集合. 多変数多項式環の単項式順序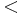 を固定する. このとき,有限個の
を固定する. このとき,有限個の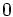 でない多変数多項式の集合である グレブナー基底
でない多変数多項式の集合である グレブナー基底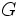 は, 任意の
は, 任意の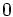 でない多変数多項式
でない多変数多項式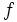 を
を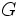 の元で 割ったときに, 割り算の順序によらず余りが一意となる良い性質をもつ. グレブナー基底は,ブッフバーガーアルゴリズムと呼ばれる解法で計算される.
の元で 割ったときに, 割り算の順序によらず余りが一意となる良い性質をもつ. グレブナー基底は,ブッフバーガーアルゴリズムと呼ばれる解法で計算される.
詳説
グレブナー基底 (Gröbner basis) は,体上の多変数多項式環の上で定義される「性質の良い」多項式の集合で,多変数からなる連立代数方程式の求解等に適用される.多項式環のイデアルのグレブナー基底の概念は,1960年代,オーストリアの大学院生であったブッフバーガー (Bruno Buchberger) によって発表された.ブッフバーガーは指導教官のグレブナー(Wolfgang Gröbner) に敬意を表しグレブナー基底と名付けている.ブッフバーガーは,学位論文で多項式環の剰余類環を計算する未解決問題に対し,グレブナー基底の概念とグレブナー基底を求める算法であるブッフバーガー算法 (Buchberger's algorithm) を示して解決を図った.なお,同時期に広中平祐が,局所環のイデアルに対して同様の概念 (標準基底) を独立に導入している.
グレブナー基底に関する研究は,コンピュータの飛躍的な進歩と計算代数の研究の発展と共に盛んになり今日に至る.現在,グレブナー基底は可換代数,代数幾何,微分方程式等の純粋数学のみならず,組合せ論,凸多面体の三角形分割,符号,統計,整数計画等の情報科学や応用分野にも影響を及ぼしている.Mathematica, Maple, Risa/Asir, Singular, Macaulay 2 等の数式処理システムには,標準でグレブナー基底を計算するパッケージが組み込まれており,さらに,複数の研究者グループがグレブナー基底計算を含む計算機代数システムの開発を手掛けている.
多変数の連立代数方程式を解くには,等価でかつ解きやすい形の別の連立方程式を求める必要があり,そこに表れる多項式がグレブナー基底である.多変数代数方程式の解の存在の判定には,多項式イデアル (以後イデアルと呼ぶ) という多項式集合が用いられる.イデアルは,多変数多項式の連立代数方程式の一般化で,多項式環の任意のイデアルに対してグレブナー基底が存在する事が知られている.グレブナー基底を計算する際には,多項式中の各単項式の「全順序」を考慮する必要があるため,ここで単項式順序について触れる.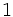 変数多項式内の各単項式の全順序は,変数の次数を用いて順序付け出来る.しかし,
変数多項式内の各単項式の全順序は,変数の次数を用いて順序付け出来る.しかし,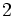 変数以上の多項式で各単項式に全順序を定義するには,順序規則を導入しなければならない.この規則は単項式順序 (monomial order),項順序(term order)等と呼ばれる.(グレブナー基底に関する用語や記号は,統一されていないものが多いことに注意されたい.)一般に, 単項式順序は以下の二つの条件を満たすものと定義される.すなわち,「(1) 任意の単項式
変数以上の多項式で各単項式に全順序を定義するには,順序規則を導入しなければならない.この規則は単項式順序 (monomial order),項順序(term order)等と呼ばれる.(グレブナー基底に関する用語や記号は,統一されていないものが多いことに注意されたい.)一般に, 単項式順序は以下の二つの条件を満たすものと定義される.すなわち,「(1) 任意の単項式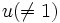 は
は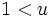 を満たす」,「(2) 単項式
を満たす」,「(2) 単項式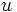 と
と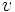 が
が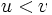 であるならば,任意の単項式
であるならば,任意の単項式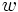 について,
について,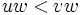 である」というものである.単項式順序には,辞書式順序,次数付き辞書式順序,次数付き逆辞書式順序等がある.
である」というものである.単項式順序には,辞書式順序,次数付き辞書式順序,次数付き逆辞書式順序等がある.
ブッフバーガー算法は,任意のイデアルの生成系のグレブナー基底を計算するアルゴリズムで,ユークリッドの互除法の一般化のような算法である.入力として「イデアルの基底」と呼ばれる多項式の集合と,多項式中の各単項式に対する「単項式順序」が与えられると,単項式順序に関するグレブナー基底が出力されるのである.
ブッフバーガー算法を説明する前に,算法中で用いる操作等を定義する.多項式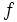 を多項式
を多項式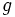 で簡約するとは,「
で簡約するとは,「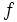 中の単項式」から「
中の単項式」から「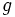 中の単項式順序の一番大きな項で割り切れるもの」を消すことである.多項式
中の単項式順序の一番大きな項で割り切れるもの」を消すことである.多項式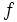 を多項式の集合
を多項式の集合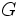 で簡約するとは,
で簡約するとは,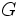 の各元を前出の
の各元を前出の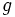 として
として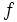 に適用することである.
に適用することである.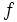 を
を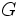 のどの元でも簡約出来ない時,
のどの元でも簡約出来ない時,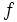 は正規形であるといい, 簡約を繰り返して正規形を得ることを正規化という.
は正規形であるといい, 簡約を繰り返して正規形を得ることを正規化という.
ブッフバーガー算法 (Buchberger's Algorithm)
算法中の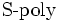 の正確な定義は紙面の都合割愛する.詳細は参考文献を参照されたい.グレブナー基底は単項式順序に依存し,単項式順序が異なると,求まるグレブナー基底も異なるかもしれない.一般に,多項式
の正確な定義は紙面の都合割愛する.詳細は参考文献を参照されたい.グレブナー基底は単項式順序に依存し,単項式順序が異なると,求まるグレブナー基底も異なるかもしれない.一般に,多項式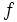 を複数の多項式
を複数の多項式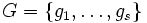 で正規化する場合,
で正規化する場合,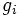 を選ぶ順序によって正規形が異なるが,
を選ぶ順序によって正規形が異なるが,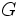 がグレブナー基底であれば
がグレブナー基底であれば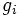 を選ぶ順序によらず正規形の一意性が保証される.
を選ぶ順序によらず正規形の一意性が保証される.
ブッフバーガー算法では,計算途中で生成元が膨れ上がり,最終的にグレブナー基底として選ばれる元は,計算途中で求めた生成元の一部である.ブッフバーガー算法で求まるグレブナー基底には一意性がなく,冗長な元が含まれているが,不要な元を取り除く等の操作を施すことにより被約グレブナー基底 (reduced Gröbner basis)と呼ばれる一意なグレブナー基底を求めることが出来る.
ブッフバーガー算法によるグレブナー基底の計算時間は,単項式順序に依存する.例えば,辞書式順序のグレブナー基底を求める場合,他の単項式順序のグレブナー基底を計算してから,「基底変換」操作を行って,辞書式順序のグレブナー基底を求める方が,直接辞書式順序のグレブナー基底を計算するよりも効率が良い場合があることが経験的に知られている.そのため,近年,基底変換に関する算法研究が注目されている.
ここで,グレブナー基底を用いた整数計画問題の求解の概要について触れる.まず問題を標準化し,等式制約から多変数多項式系を生成する.次に,目的関数のコストベクトルから単項式順序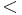 を決定する.この多変数多項式系と単項式順序
を決定する.この多変数多項式系と単項式順序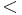 を入力とし,グレブナー基底
を入力とし,グレブナー基底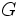 を計算する.すると,整数計画問題の制約式の右辺項ベクトルから生成される単項式を
を計算する.すると,整数計画問題の制約式の右辺項ベクトルから生成される単項式を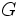 で正規化して得られた正規形から,容易に最適解を導くことが出来る.
で正規化して得られた正規形から,容易に最適解を導くことが出来る.
グレブナー基底は,列挙やサンプリングとも密接な関係がある.グレブナー基底を利用して,逆探索法の枠組みで整数計画問題の実行可能領域中の実行可能解 (整数点) の列挙や,マルコフ連鎖構築による整数点のサンプリングが実現出来ることが知られている[9].そのため,今後,グレブナー基底と凸多面体との関連研究の発展が期待される.
グレブナー基底に関する文献は代数の予備知識を仮定したものが多いが,文献 [6] は非数学者向けにグレブナー基底とその周辺知識が記述され,初学者に適している.実際に計算機でグレブナー基底を計算する際には,文献 [8] が参考になる.
[1] W. Adams and P. Loustaunau, An Introduction to Gröbner Bases, Graduate Studies in Mathematics, 3, American Mathematical Society, Providence, RI, 1994.
[2] P. Conti and C. Traverso, "Buchberger algorithm and integer progamming," in Applied Algebra, Algebraic Algorithms and Error-correcting codes(AAECC-9), H. Mattson, T. Mora and T. Rao, eds., Lecture Notes inComputer Science 539, Springer-Verlag, New York, 130-139, 1991.
[3] D. Cox, J. Little and D. O'Shea, "Ideals,Varieties, and Algorithms," Springer-Verlag, New York, 1992. 落合啓之, 示野信一, 西山享, 室政和, 山本敦子共訳,『グレブナー基底と代数多様体入門 上,下』, シュプリンガー・フェアラーク東京, 2000.
[4] D. Cox, J. Little and D. O'Shea, "Using Algebraic Geometry," Springer-Verlag, New York, 1998. 大杉英史, 北村知徳,日比孝之共訳,『グレブナー基底 1,2』, シュプリンガー・フェアラーク東京, 2000.
[5] 日比孝之,『グレブナー基底』, 野海正俊・日比孝之編, すうがくの風景 8, 朝倉書店, 2003.
[6] 平林隆一,『工学基礎 代数系とその応用』, 数理工学社, 2006.
[7] S. Hosten and R. R. Thomas, "Gröbner Bases and Integer Programming, in Gröbner Bases and Applications, Proc. of 33 Years of Groebner Bases Conference, B. Buchberger and F. Winkler, eds., London Mathematical Society Lecture Note Series 251, Cambridge University Press, Cambridge, 144-158, 1998.
[8] 野呂正行,横山和弘,『グレブナー基底の計算 基礎篇 計算代数入門』, 東京大学出版会, 2003.
[9] B. Sturmfels, Gröbner Bases and Convex Polytopes, University Lecture Notes Series, 8, American Mathematical Society, Providence, RI, 1995.
[10] R. R. Thomas, "Gröbner Bases in Integer Programming," in Handbook of Combinatorial Optimization Vol.1, D. -Z. Du and P. M. Pardalos, eds., Kluer Academic Publishers, 1998.
ぐれぶなーきていと同じ種類の言葉
- ぐれぶなーきていのページへのリンク
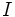 の
の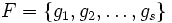 ,
,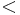
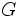
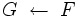
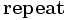
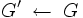
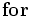 各
各 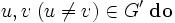
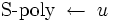 と
と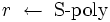 を
を