BCCモデル
【英】:BCC (Banker, Charnes and Cooper) model
概要
DEA (包絡分析法) のモデルとしてバンカー・チャーンズ・クーパーにより提案され, 3人の頭文字をとって名づけられたモデルである. 生産可能集合は現存するDMUの凸包とそれより大きい入力と小さい出力をもつ点から構成される. このモデルはCCRモデルと異なり, 効率的フロンティアは通常原点を通らず, 規模の収穫は可変型である.
詳説
DEA(包絡分析法)のモデルとしてBanker, Charnes andCooperにより提案され, 3人の頭文字をとって名づけられたモデルである[1].
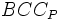 -I モデルは
-I モデルは
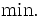 |
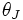 |
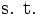 |
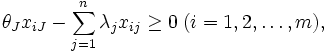 |
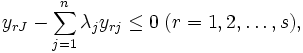 |
|
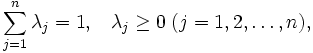 |
で表わされる. 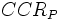 -Iモデルと比べると制約
-Iモデルと比べると制約 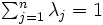 が追加されたモデルになっている. これにより生産可能集合は, DMU集合の凸包を基本とし, その凸包の点より大なる入力と小なる出力を持つ点から構成されることになる.
が追加されたモデルになっている. これにより生産可能集合は, DMU集合の凸包を基本とし, その凸包の点より大なる入力と小なる出力を持つ点から構成されることになる.
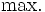 |
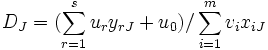 |
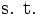 |
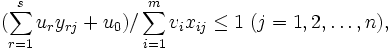 |
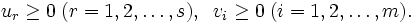 |
CCRモデルでは上式の分子の定数項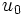 がないため分母分子を定数倍しても効率は変わらない. すなわち, CCRモデルではすべての入力, 出力を
がないため分母分子を定数倍しても効率は変わらない. すなわち, CCRモデルではすべての入力, 出力を 倍しても効率は変わらないので規模の収穫が一定であるといわれる. これに対し, BCCモデルでは小規模の段階では規模の収穫が増加し, 規模の増加に連れて規模の収穫は一定レベルに到達する. それよりも規模が大きくなると規模の収穫が減少する.
倍しても効率は変わらないので規模の収穫が一定であるといわれる. これに対し, BCCモデルでは小規模の段階では規模の収穫が増加し, 規模の増加に連れて規模の収穫は一定レベルに到達する. それよりも規模が大きくなると規模の収穫が減少する.
BCCモデルはCCRモデルよりも制約が多いため生産可能集合が狭められて効率値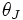 (BCC)はCCRモデルの効率値
(BCC)はCCRモデルの効率値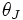 (CCR)以上になる. そこで
(CCR)以上になる. そこで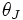 (CCR)を全体効率性,
(CCR)を全体効率性, 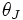 (BCC)を技術効率性と考え, その差分は規模の効率性によるものと考え, 規模の効率性=全体効率性
(BCC)を技術効率性と考え, その差分は規模の効率性によるものと考え, 規模の効率性=全体効率性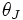 (CCR)÷技術効率性
(CCR)÷技術効率性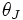 (BCC)とする. すなわち, 全体効率性(CCR)=技術効率性(BCC)×規模の効率性と考える.
(BCC)とする. すなわち, 全体効率性(CCR)=技術効率性(BCC)×規模の効率性と考える.
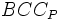 -Iモデルは入力指向型モデルであるが, 出力指向型モデルも同様に考えられる. これらに対して入力指向と出力指向を区別せずに, スラックに着目したモデルとしてDEA加法モデルがある. 基本的加法モデルは次のLPによって示される.
-Iモデルは入力指向型モデルであるが, 出力指向型モデルも同様に考えられる. これらに対して入力指向と出力指向を区別せずに, スラックに着目したモデルとしてDEA加法モデルがある. 基本的加法モデルは次のLPによって示される.
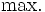 |
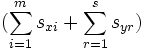 |
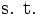 |
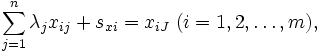 |
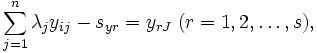 |
|
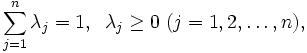 |
|
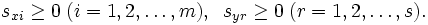 |
Cobb-Douglas型の生産関数
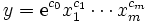
または
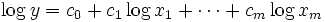
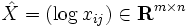
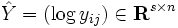
を入出力データとした加法モデルは原データに戻したときに積で表現できることからDEA乗法モデルと呼ばれる.
[1] R. D. Banker, A. Charnes and W. W. Cooper, "Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis," Management Science, 30 (1984), 1078-1092.
- BCCモデルのページへのリンク
