双曲線
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/04/09 08:17 UTC 版)
|
|

|
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月)
翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|

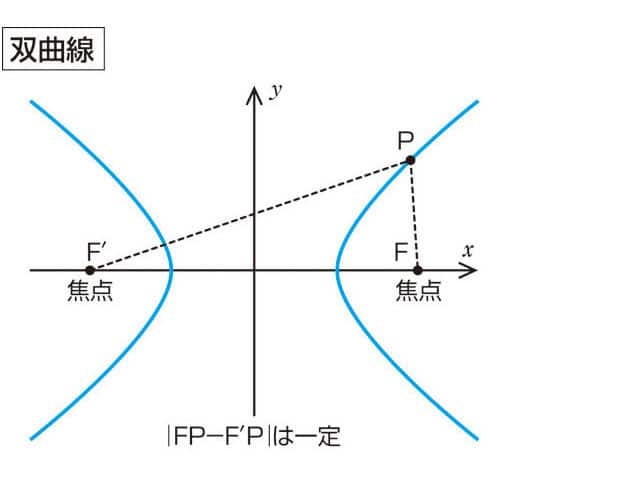
双曲線(そうきょくせん、英: hyperbola)とは、2次元ユークリッド空間 ℝ2 上で定義され、ある2点 F, F' からの距離の「差が一定」であるような曲線の総称である。
この2点 F, F' は焦点と呼ばれる。2点 F, F' を通る直線と2点 F, F' の垂直二等分線は主軸と呼ばれる。
双曲線の方程式
一般形
標準形
| 標準形 | 
双曲線は、直円錐を直円錐の頂点を通らず、上下両方の直円錐に交わる平面で切断したときの、切断面の境界である。 離心率が e であるような円錐曲線を Ce とする。このとき、e > 1 であれば、 Ce は双曲線となる。この円錐曲線を適当に直交変換することにより、準線が x = −f , 焦点の一つが F(f, 0) となったとする。双曲線の任意の点 P(x, y) に対し、方程式 |
|---|
双曲線
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/11/15 08:07 UTC 版)
双曲線では、軌道長半径とは2つの分岐の間の半分の距離である。a が x 軸方向にあるとすると、 ( x − h ) 2 a 2 − ( y − k ) 2 b 2 = 1 {\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1} となる。半通径と離心率を使うと、 a = ℓ e 2 − 1 {\displaystyle a={\frac {\ell }{e^{2}-1}}} と書ける。双曲線の主軸は、軌道長半径と同じ方向である。
※この「双曲線」の解説は、「軌道長半径」の解説の一部です。
「双曲線」を含む「軌道長半径」の記事については、「軌道長半径」の概要を参照ください。
「双曲線」の例文・使い方・用例・文例
双曲線と同じ種類の言葉
- 双曲線のページへのリンク