多重共線性

統計学用語辞典

多重共線性 multicollinearity

　通称「マルチコ」。独立変数間に非常に強い相関があったり，一次従属な変数関係がある場合には，解析が不可能（「逆行列が求まりません」というエラーメッセージが出力される）であったり，たとえ結果が求まったとしてもその信頼性は低い。このような場合に多重共線性があると言われる。
詳しくは，重回帰分析を参照のこと。

多重共線性

　変数選択を行わない場合には，独立変数相互間に相関の高いものは含めないほうがよい。
　もし，それらの中に独立でないものが含まれていると（ 例えば変数 A，B とその合計値 C = A + B が共に含まれていると ）分析は失敗する。
　場合によっては，各独立変数と従属変数との相関係数の符号と，偏回帰係数の符号が一致しない場合が生ずる。これは，「予測を行う」という観点から偏回帰係数が定められるので，重回帰式に含まれた変数相互間の関連で符号が決められるためである。このようなことが起きるのは，独立変数間に相関の高いものが混ざっていることが原因である（ ある変数で予測しすぎた部分を別の変数で打消しているような場合がある ）。しかし，このようなことは因果関係を考える上では不都合なので，符号が一致しない独立変数を除いた重回帰式を探索するとよいであろう。
　独立変数間の相関係数行列の逆行列の要素を rⁱⁱ としたとき，

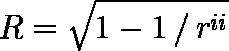
は，独立変数 i を残りの独立変数で予測するときの重相関係数になっている。したがって，この数値が大きいものは独立変数としてふさわしくないことを表す。
　これと同じことであるが 1 / rⁱⁱ を トレランス，rⁱⁱ を 分散拡大係数 と呼ぶことがある。この場合には，トレランスが低い（ 分散拡大係数が大きい ）独立変数は除く方がよいことを表す。