補集合

デジタル大辞泉

ほ‐しゅうごう〔‐シフガフ〕【補集合】

読み方：ほしゅうごう

ある集合Aが全体集合Uの部分集合であるとき、ある集合を全体集合から除いたあとの集合。余集合。

算数用語集・数学用語集

補集合

ある集合 A に対して全体集合 U の要素から集合 A の要素を除いてできる要素の集合を A の補集合という。

ウィキペディア

差集合

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/03/28 05:51 UTC 版)

差集合（さしゅうごう、英: set difference）とは、ある集合の中から別の集合に属する要素を取り去って得られる集合のことである。特に、全体集合 U を固定して、U からその部分集合 A の要素を取り去って得られる集合を A の補集合という。

定義

差集合 B − A のベン図による視覚化（左が A、右がB。）:
$B\setminus A~~=~~A^{c}\cap B$

差集合 A − B のベン図による視覚化（左が A、右がB。）:
$A\setminus B~~=~~A\cap B^{\mathrm {c} }$

補集合のベン図による視覚化（左がA、右がB。）:
$A^{c}~~=~~\emptyset ^{c}\setminus A$ カテゴリ

ウィキペディア小見出し辞書

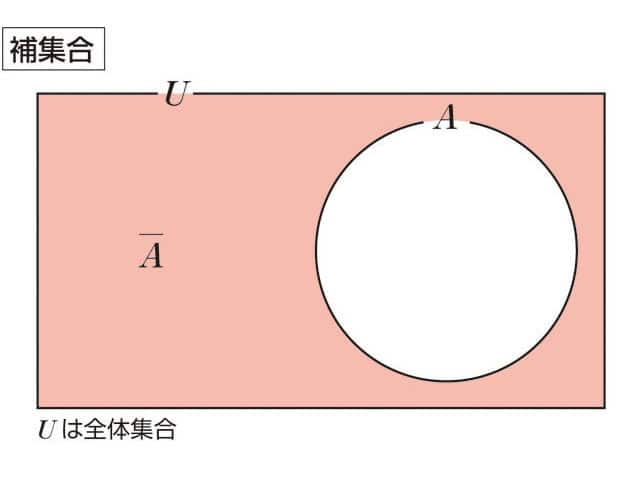
補集合

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/07/17 07:48 UTC 版)

「差集合」の記事における「補集合」の解説

補集合のベン図による視覚化（左がA、右がB。）: A c     =     ∅ c ∖ A 全体集合や普遍集合 (universe) などと呼ばれる（大きな）集合 U を固定して、その部分集合についてのみ考えているとき（例えば、U が自然数全体、実数全体やある位相空間であるときなど） U の部分集合 A について、 U ∖ A を A の（絶対）補集合（ほしゅうごう、complement）といい、Uが了解されている文脈では単に A c , ∁ A , A ¯ などと表す。 ある集合の補集合の補集合はもとの集合自身である。 自然数について考えているとき、奇数全体の集合の補集合は偶数全体の集合である。 実数全体 R について考えているとき、有理数全体 Q の補集合 R ∖ Q は無理数全体である。

Wiktionary日本語版（日本語カテゴリ）

補集合

出典:『Wiktionary』 (2020/03/11 13:46 UTC 版)

名詞

補 集合（ほしゅうごう）

1. 固定された全体集合の要素から、その全体集合に含まれる部分集合の要素を取り除いて作る差集合。例えば、全体集合を実数 R 全体、取り除く部分集合を有理数 Q とすると、補集合 Q^c は無理数全体となる。

関連語

• 空集合
• 和集合

翻訳

• 英語：complement