例題の答え

統計学用語辞典

例題の答え

　各変数において，平均値からの偏差を計算すると，表 1 のようになる。

表 1．平均値からの偏差および予測値

ケース番号	X1	X2	Y	X1-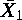	X2-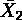	Y-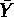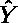
1	1.2	1.9	0.9	-4.2	-1.4	-1.3	0.939
2	1.6	2.7	1.3	-3.8	-0.6	-0.9	1.250
3	3.5	3.7	2.0	-1.9	0.4	-0.2	1.926
4	4.0	3.1	1.8	-1.4	-0.2	-0.4	1.856
5	5.6	3.5	2.2	0.2	0.2	0.0	2.298
6	5.7	7.5	3.5	0.3	4.2	1.3	3.465
7	6.7	1.2	1.9	1.3	-2.1	-0.3	1.864
8	7.5	3.7	2.7	2.1	0.4	0.5	2.744
9	8.5	0.6	2.1	3.1	-2.7	-0.1	2.060
10	9.7	5.1	3.6	4.3	1.8	1.4	3.596
平均値	5.4	3.3	2.2

　正規方程式は，
　　　　71.98b1 + 6.46b2 = 16.58
　　　　6.46b1 + 35.30b2 = 11.44
となり，これを解いて，b1 = 0.20462，b2 = 0.28663 となる。
　また，b0 = 2.2 - 0.20462・5.4 - 0.28663・3.3 = 0.14918 となる。
　すなわち，求める重回帰式は 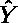= 0.20462 X1 + 0.28663 X2 + 0.14918 である。
　標準化偏回帰係数は，Syy = 6.7 であるから，
　b1' = 0.20462 √ ( 71.98 / 6.7 ) = 0.67067，
　b2' = 0.28663 √ ( 35.3 / 6.7 ) = 0.65793 である。
　偏回帰係数が 0 であるという帰無仮説の検定に用いる t 値は，それぞれ 27.05056，26.53645 となり（ 自由度 7 の t 分布に従う ），帰無仮説は棄却される。また，定数項が 0 の検定の t 値は 2.73685 で，同じく帰無仮説は棄却される（ 有意水準 5% ）。
　分散分析は表 2 のようになる。

表 2．分散分析表

要因	平方和	自由度	平均平方	F値	有意確率
回帰	6.67164	2	3.33582	823.47652	＜ 0.00001
残差	0.02836	7	0.00405
全体	6.70000	9	0.74444

　重相関係数の 2 乗は，R² = 1 - 0.02834 / 6.70000 = 0.99577 となる。