母平均の検定区間推定のとき

統計学用語辞典

母平均の検定・区間推定のとき

　信頼率 ( 1 - α ) のもとで，母平均 μ を ± d の精度で推定するために必要な標本の大きさ n は，(1)式で見積もることができる。
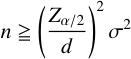　…… (1)
例：
　類似の過去の調査結果から，母平均が 10，母分散が 3 程度であると考えられる。このとき，信頼率 95% で母平均を ±0.5 の精度で推定するためにはどのくらいの標本が必要か。
答え：
　α = 0.05 であるから，Zα / 2 = Z0.025 ≒ 1.96 となる。したがって，
　　n ≒ (1.96 / 0.5)² × 3 = 46.0992


(1)式はいろいろな教科書に載っているものであるが，検出力を指定できないので，場合によっては不都合である。
検出力を指定して必要な標本の大きさを求めるには，(2)式を使う。
ちなみに，(1)式と(2)式を比較してみると，分子に Z β が含まれているかどうかの違いであり，上に示した式で得られるのは検出力が 50% のときのものであることがわかる（Zβ = Z0.5 = 0)。
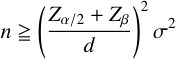　…… (2)
上の例題を，検出力 = 0.8 として解いてみよう。
1-β = 0.8 すなわち，β = 0.2 であるから，Zβ = Z0.2 ≒ 0.8416 となる。したがって，
　　n ≒ { (1.96 + 0.8416) / 0.5}² × 3 = 94.18755

　　東京大学教養学部統計学教室編「基礎統計学III　自然科学の統計学」東京大学出版会