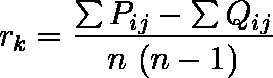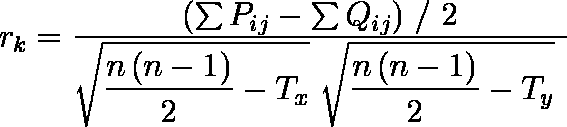ケンドールの順位相関係数

統計学用語辞典

ケンドールの順位相関係数

例題：
　「表 1 において，変数 X と変数 Y の間のケンドールの順位相関係数を求めなさい。」

表 1．二変数データ

i	1	2	3	4	5	6	7	8	9	10
変数 Xi	2.8	3.4	3.6	5.8	7.0	9.5	10.2	12.3	13.2	13.4
変数 Yi	0.6	3.0	0.4	1.5	15.0	13.4	7.6	19.8	18.3	18.9

計算手順：

1. ケース数を n とする。
   
2. 変数 X と変数 Y について小さい方から順位をつけ，変数 X について小さい順に並べ変える（同順位の場合には平均順位をつける）。
   
3. Yi（ i = 1， 2， ... ， n - 1 ）について，Yi ＜ Yj の個数を Pi ，Yi ＞ Yj の個数を Qi とする（ j = i + 1，i + 2， ... ，n ）。
   例えば，表 2 に示すように，X5 に対する Y の順位は 7 であり，それより右にある Y の順位のうち，大きいものは Y8 ，Y9 ，Y10 の 3 個（ P5 = 3 ），小さいものは Y6 ，Y7 の 2 個（ Q5 = 2 ）。
   Pi + Qi = n - i ，Σ ( Pi + Qi ) = n ( n - 1 ) / 2 となることに注意。
   
4. Σ Pi は 2 変数の順位の方向が一致する回数，Σ Qi は 2 変数の順位の方向が逆方向に一致する回数なので，Σ Pi - Σ Qi は順序の一致性の指標である。
   
   • 2 変数の順序が完全に一致するときには，Σ Pi = n (n - 1) / 2，Σ Qi = 0 である。
     
   • 2 変数の順序が逆順に完全に一致するときには，Σ Pi = 0，Σ Qi = n (n - 1) / 2 である。
   
   このようなことから，次式を定義すれば， - 1 ≦ rk ≦ 1 となる。これがケンドールの順位相関係数である。
   
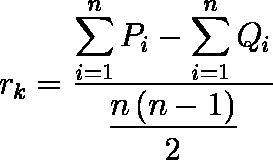
   例題では，Σ Pi = 37，Σ Qi = 8 なので，rk = ( 37 - 8 ) / ( 10・9 / 2 ) = 0.64444 となる。
   
   • 相関係数が正の場合「二変数には正の相関関係がある」という（正相関）
   • 相関係数が負の場合「二変数には負の相関関係がある」という（負相関）
   • 相関係数が０に近いとき「二変数は無相関である」という

表 2．ケンドールの順位相関係数の計算例

i	1	2	3	4	5	6	7	8	9	10
変数 Xi の順位	1	2	3	4	5	6	7	8	9	10
変数 Yi の順位	2	4	1	3	7	6	5	10	8	9
Pi	8	6	7	6	3	3	3	0	1		Σ Pi = 37
Qi	1	2	0	0	2	1	0	2	0		Σ Qi = 8
Pi+Qi	9	8	7	6	5	4	3	2	1		Σ ( Pi + Qi ) = 45

注：

• どちらか一方（または両方）の変数において全てのケースが同一の値をとる場合には，相関係数は定義できない。
  
• 同順位がある場合には，変数 X，変数 Y における同順位の個数を nx ，ny ，同順位の大きさを ti ，tj（ i = 1，2， ... ，nx ；j = 1，2， ... ，ny ）としたとき，次式で計算される。同順位がない場合には Tx = Ty = 0 となり，前式に等しい。
  
  
  
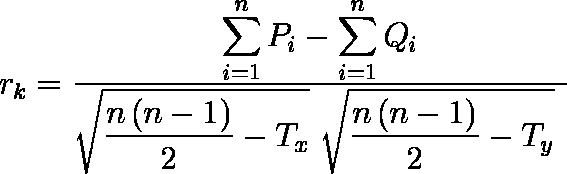
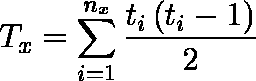
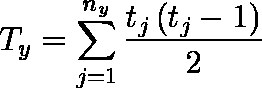
  注意：上の定義では，変数 X と変数 Y のいずれかに（両方に）同順位があるかで取り扱いが曖昧になることがある。
  そこで，ケンドールの順位相関係数のもう一つの定義法を示しておく（同順位がない場合は同じ結果が得られる。また，この方法では順位付けをする必要はない）。
  変数の組 ( Xi ，Yi ）と ( Xj ，Yj ）を考える（ i ≠ j ）。
  
  • Xi ＞ Xj かつ Yi ＞ Yj のとき Pij = 1
  • Xi ＜ Xj かつ Yi ＜ Yj のとき Pij = 1
  • Xi ＞ Xj かつ Yi ＜ Yj のとき Qij = 1
  • Xi ＜ Xj かつ Yi ＞ Yj のとき Qij = 1
  
  として，Σ Pij - Σ Qij を求める。
  
  • 同順位がないとき
    　　
    
  • 同順位があるとき
    　　
    　　Tx ， Ty は前述の通り。