maximum cut problem

OR事典

最大カット問題

読み方：さいだいかっともんだい
【英】：maximum cut problem

無向グラフ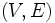において, 各枝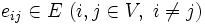に非負整数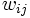が重みとして付与されている. このとき

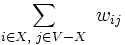
を最大にする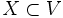を求める問題. つまり, を2つの部分集合に分割する組合せ(カット)のうち, それらの部分集合間の枝に付与された重みの総和が最大となる分割を求める.

「OR事典」の他の用語

近似・知能・感覚的手法：

導出原理  局所探索法  支配関係に基づくラフ集合  最大カット問題  欲張り法  決定表  発見的探索

ウィキペディア

最大カット問題

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2025/08/02 09:16 UTC 版)

最大カットの例。この場合、カット数は 5 である。

最大カット問題（さいだいカットもんだい、英: maximum cut problem）とは、グラフ理論における問題の一種である。あるグラフにおけるカットの中で最大のものを求める問題である。すなわち、グラフの頂点を二つの補集合 S、T に分割するとき、S、T を結ぶ辺の数が最大となるような分割を求める問題である。

また、最大カット問題は次のように述べることができる。今、頂点集合の部分集合 S を求めるとする。このとき、S とその補集合の間にある辺の本数ができるだけ多くなることを考える。あるいは、元のグラフからできるだけ多くの辺を含む二部グラフを得る問題である。

この問題には重み付き最大カット問題（weighted max-cut）と呼ばれる最大カット問題をより一般化した問題が存在している。この場合、各辺に実数の重みが割り当てられており、目的としては部分集合 S とその補集合の間の辺の数ではなく、それらの辺の重みの総和を最大化する分割を求めることとなる。辺の重みについて負の場合も許容される場合は重み付き最大カット問題はすべての重みの符号を反転することにより、自明に重み付き最小カット問題へと変換することができる。

下界

エドワードは n 個の頂点および m 個の辺を有するグラフ G において最大カットに関する以下の下界を示した:

• 任意のグラフの場合: $\displaystyle \left\lceil {\frac {m}{2}}+{\sqrt {{\frac {m}{8}}+{\frac {1}{64}}}}-{\frac {1}{8}}\right\rceil .$
  この節は英語版の対応するページを翻訳することにより充実させることができます。（2025年7月）

  翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。

  • 英語版記事を日本語へ機械翻訳したバージョン（Google翻訳）。
  • 万が一翻訳の手がかりとして機械翻訳を用いた場合、翻訳者は必ず翻訳元原文を参照して機械翻訳の誤りを訂正し、正確な翻訳にしなければなりません。これが成されていない場合、記事は削除の方針G-3に基づき、削除される可能性があります。
  • 信頼性が低いまたは低品質な文章を翻訳しないでください。もし可能ならば、文章を他言語版記事に示された文献で正しいかどうかを確認してください。
  • 履歴継承を行うため、要約欄に翻訳元となった記事のページ名・版について記述する必要があります。記述方法については、Wikipedia:翻訳のガイドライン#要約欄への記入を参照ください。
  • 翻訳後、{{翻訳告知|en|Maximum cut#Polynomial-time algorithms|…}}をノートに追加することもできます。
  • Wikipedia:翻訳のガイドラインに、より詳細な翻訳の手順・指針についての説明があります。

  最大カット問題はNP困難であるため、現時点では最大カット問題を多項式時間で解くアルゴリズムは発見されていない。

  しかしながら、平面グラフに対する最大カット問題は平面グラフ G の最大カットに含まれない辺が、G の双対グラフにおいて最適な閉路の中で重複して通過される辺の双対辺に対応するため、中国人郵便配達問題（グラフの辺を少なくとも一回ずつ辿る最短の閉路を求める問題）と双対の関係にある。

  近似アルゴリズム

  最大カット問題はAPX困難であることが知られているため、P=NP でない限り最適解に十分に近しい解を求めるような多項式時間近似スキーム（PTAS）が存在しないとされている。このことから、現在知られているすべての多項式時間アルゴリズムについて1より小さな近似比しか示さない。

  最大カット問題は次の単純な乱択アルゴリズムによる0.5-近似アルゴリズムが知られている: 各頂点ごとにコインを投げて、どちらか一方の分割に割り当てる。このとき、各辺がカットに含まれるかは辺のそれぞれの頂点がそれぞれ異なる分割に含まれるかによって決定されるため、このときカットの期待値は辺の半数となる。この乱択アルゴリズムは条件付確率的手法によって脱乱択となる。このことから、この単純なアルゴリズムは0.5-近似多項式時間アルゴリズムとなる。このようなアルゴリズムの一つの例としてはある与えられたグラフ $G=(V,E)$

  この節は英語版の対応するページを翻訳することにより充実させることができます。（2025年7月）

  翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。

  • 英語版記事を日本語へ機械翻訳したバージョン（Google翻訳）。
  • 万が一翻訳の手がかりとして機械翻訳を用いた場合、翻訳者は必ず翻訳元原文を参照して機械翻訳の誤りを訂正し、正確な翻訳にしなければなりません。これが成されていない場合、記事は削除の方針G-3に基づき、削除される可能性があります。
  • 信頼性が低いまたは低品質な文章を翻訳しないでください。もし可能ならば、文章を他言語版記事に示された文献で正しいかどうかを確認してください。
  • 履歴継承を行うため、要約欄に翻訳元となった記事のページ名・版について記述する必要があります。記述方法については、Wikipedia:翻訳のガイドライン#要約欄への記入を参照ください。
  • 翻訳後、{{翻訳告知|en|Maximum cut#Parameterized algorithms and kernelization|…}}をノートに追加することもできます。
  • Wikipedia:翻訳のガイドラインに、より詳細な翻訳の手順・指針についての説明があります。

  応用

  機械学習

  頂点を特徴量、辺を特徴量間の距離とみなすことで、最大カット問題に対するアルゴリズムはそれらの特徴量を二つのクラスに分類することができる。言い換えれば、自然に二値分類される。最大カットアルゴリズムは他のアルゴリズムと比較すると、特徴量空間を定義する必要がなく、特徴量間の距離のみを与えることでアルゴリズムにより分割を実行することができる。

  理論物理学

  統計力学・無秩序系において最大カット問題はスピングラス模型あるいはより単純化したイジング模型におけるハミルトニアンの最小化に等しい。グラフ G でのイジング模型および最隣接相互作用に対してハミルトニアンは $H[s]=-\sum _{ij\in E(G)}J_{ij}s_{i}s_{j}$ カテゴリ / コモンズ

Weblio日本語例文用例辞書

「maximum cut problem」の例文・使い方・用例・文例

• Calcutta は小ロンドンだ
• Calcutta は小規模の London だ
• ‘problem' と ‘question' はどちらを用いてもよいことがある 《同じ意味のことがある》.