双対性理論
【英】:duality theory
概要
非線形計画のみならず線形計画, 多目的計画, 離散凸解析などの分野で主問題とその双対問題の関係および集合や関数の双対関係を説明する重要な基礎理論. 共役関数やラグランジュ関数の性質に基づいていて, 鞍点定理やミニマックス定理と密接に関係している.
詳説
双対性理論 (duality theory)は,非線形計画のみならず線形計画,多目的計画,離散凸解析などの分野で主問題とその双対問題の関係,および集合や関数の双対関係を説明する重要な基礎理論である [1, 2, 3, 4].
「双対」 (dual) と「共役」 (conjugate) は元々同義語として用いられ,数学の関数解析の分野では,ノルム空間 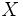 上の有界線形汎関数の全体を
上の有界線形汎関数の全体を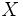 の双対空間 (dual space) または共役空間 (conjugate space) といい,
の双対空間 (dual space) または共役空間 (conjugate space) といい,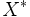 と表して,
と表して,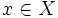 における
における 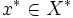 の値を
の値を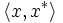 または
または 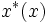 と書く.
と書く.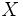 が
が  次元実ユークリッド空間
次元実ユークリッド空間 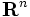 の場合は,
の場合は,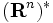 と
と 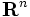 は同一視でき,
は同一視でき,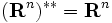 となり,
となり,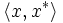 は
は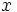 と
と 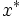 の内積
の内積 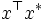 となる.以下に述べる事柄は,無限次元空間に対しても拡張できるが,ここでは簡単のため
となる.以下に述べる事柄は,無限次元空間に対しても拡張できるが,ここでは簡単のため 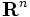 に限定して説明する.
に限定して説明する.
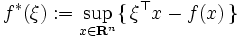 |
で定義される関数 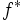 を
を 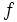 の共役関数 (conjugate function) という.共役関数
の共役関数 (conjugate function) という.共役関数 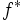 に対して,さらにその共役関数
に対して,さらにその共役関数 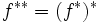 を考えることができるが,
を考えることができるが,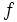 が下半連続な真凸関数のときには,
が下半連続な真凸関数のときには,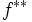 は
は 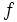 に一致する.
に一致する.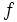 に
に 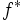 を対応させる写像をルジャンドル-フェンシェル変換 (Legendre-Fenchel transform) と呼ぶ.
を対応させる写像をルジャンドル-フェンシェル変換 (Legendre-Fenchel transform) と呼ぶ.
下半連続な真凸関数 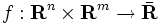 に対して,次の問題(P)と(D)を主問題 (primal problem) とその双対問題 (dual problem) と呼ぶ [4].
に対して,次の問題(P)と(D)を主問題 (primal problem) とその双対問題 (dual problem) と呼ぶ [4].
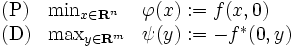 |
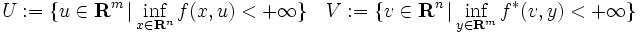 |
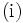
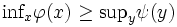
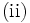
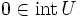 または
または 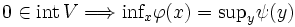
ここで,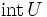 は
は 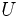 の内部を表す.(i)を弱双対定理 (weak duality theorem),(ii)を双対定理 (duality theorem) と呼び,
の内部を表す.(i)を弱双対定理 (weak duality theorem),(ii)を双対定理 (duality theorem) と呼び,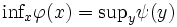 が満たされるとき,主問題(P)と双対問題(D)の間に双対性 (duality) が成立するという.(i)により,
が満たされるとき,主問題(P)と双対問題(D)の間に双対性 (duality) が成立するという.(i)により,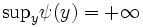 なら主問題(P)は実行可能解を持たないが,
なら主問題(P)は実行可能解を持たないが,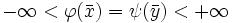 となる
となる 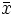 と
と 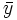 が存在すれば,それぞれ(P)と(D)の最適解となり,強い意味の双対性が成立する.一方,
が存在すれば,それぞれ(P)と(D)の最適解となり,強い意味の双対性が成立する.一方,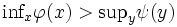 となるとき,主問題と双対問題の間に双対性のギャップ (duality gap) が存在するという.
となるとき,主問題と双対問題の間に双対性のギャップ (duality gap) が存在するという.
主問題(P)において,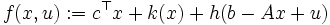 (ただし,
(ただし,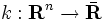 と
と 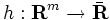 は下半連続な真凸関数で
は下半連続な真凸関数で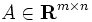 ,
, 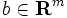 ,
, 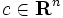 )とすると,
)とすると,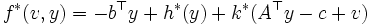 となり [4],主問題(P)と双対問題(D)はそれぞれ
となり [4],主問題(P)と双対問題(D)はそれぞれ
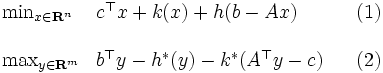 |
となる.ここで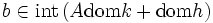 または
または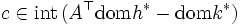 が成立すれば,(ii)により主問題 (1) と双対問題 (2) の間に双対性が成立する.(ただし,dom は拡張実数値関数の実効定義域を表す.)これをフェンシェルの双対性 (Fenchel duality) と呼んでいる.通常は,簡略化して
が成立すれば,(ii)により主問題 (1) と双対問題 (2) の間に双対性が成立する.(ただし,dom は拡張実数値関数の実効定義域を表す.)これをフェンシェルの双対性 (Fenchel duality) と呼んでいる.通常は,簡略化して 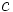 と
と 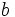 を零ベクトル,
を零ベクトル,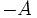 を恒等写像として,新たに
を恒等写像として,新たに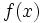 を凸関数
を凸関数 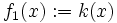 と凹関数
と凹関数 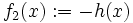 の差で表し,主問題
の差で表し,主問題 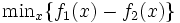 に対して,
に対して,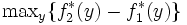 をフェンシェルの双対問題 (Fenchel dual problem) と呼ぶ.ただし,
をフェンシェルの双対問題 (Fenchel dual problem) と呼ぶ.ただし,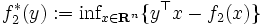 .双対性は
.双対性は 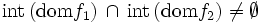 のとき成立する.また,
のとき成立する.また,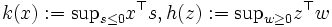 とすると,(1) と(2) は線形計画の主問題と双対問題となる [2, 4].
とすると,(1) と(2) は線形計画の主問題と双対問題となる [2, 4].
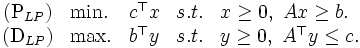 |
次に,ラグランジュ関数 (Lagrangian function) を
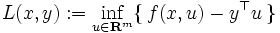 | 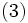 |
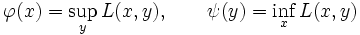 | 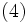 |
となる.通常,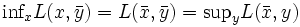 すなわち,すべての
すなわち,すべての 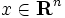 と
と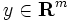 に対して
に対して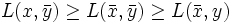 が成り立つとき,
が成り立つとき,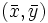 を関数
を関数 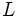 の
の  上での鞍点 (saddle point) と呼ぶ.(4) により,
上での鞍点 (saddle point) と呼ぶ.(4) により,
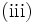
![\mbox{inf}_{x}\varphi{(x)}=\mbox{inf}_{x}\,[\,\mbox{sup}_{y}L(x,y)\,]
\ge\mbox{sup}_{y}\,[\,\mbox{inf}_{x}L(x,y)\,]=\mbox{sup}_{y}\psi{(y)}](http://weblio.hs.llnwd.net/e7/img/dict/orjtn/7df698cfd5574fa12d97b054bd9c1456.png)
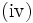
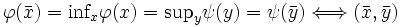 が
が の鞍点
の鞍点
が成立する.(iv) を鞍点定理 (saddle point theorem) と呼ぶ.非線形計画問題
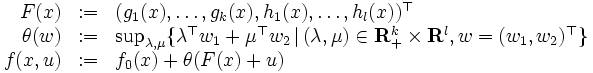 |
とおくと,(3) により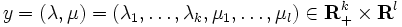 に対する問題(NLP)のラグランジュ関数は
に対する問題(NLP)のラグランジュ関数は
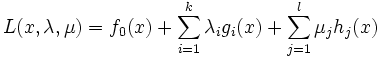 | 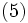 |
となる.この 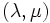 をラグランジュ乗数 (Lagrange multipliers) と呼ぶ.このとき,主問題と双対問題は
をラグランジュ乗数 (Lagrange multipliers) と呼ぶ.このとき,主問題と双対問題は
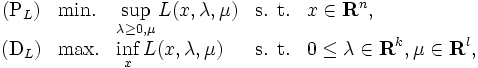 |
となり,一般に問題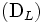 をラグランジュの双対問題 (Lagrangian dual problem)と呼ぶ.鞍点定理により,
をラグランジュの双対問題 (Lagrangian dual problem)と呼ぶ.鞍点定理により,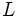 の鞍点
の鞍点 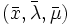 が存在すれば,つまり
が存在すれば,つまり
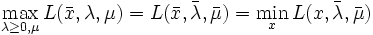 |
が成立すれば,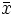 と
と 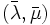 はそれぞれ問題
はそれぞれ問題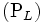 と
と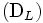 の最適解となり最適値が一致する.これをラグランジュの双対性 (Lagrangian duality) と呼ぶ.(iv) により,
の最適解となり最適値が一致する.これをラグランジュの双対性 (Lagrangian duality) と呼ぶ.(iv) により,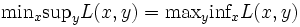 が成立すれば,この双対性が保証される.この等式に対する十分条件を述べた定理をミニマックス定理(minimax theorem) と呼ぶ [1, 2]. 逆に,主問題の目的関数
が成立すれば,この双対性が保証される.この等式に対する十分条件を述べた定理をミニマックス定理(minimax theorem) と呼ぶ [1, 2]. 逆に,主問題の目的関数 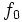 と制約関数
と制約関数 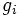 がすべて凸で,
がすべて凸で,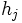 がすべてアフィン関数であるような凸計画問題 (convex programming problem) においては,適当な条件のもとで,問題
がすべてアフィン関数であるような凸計画問題 (convex programming problem) においては,適当な条件のもとで,問題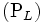 の最適解
の最適解 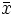 に対して,
に対して,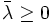 であるようなラグランジュ乗数
であるようなラグランジュ乗数 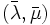 が存在して,
が存在して,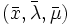 がラグランジュ関数
がラグランジュ関数 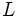 の鞍点となる.また,次のような拡張ラグランジュ関数(augmented Lagrangian function) に基づく双対性も考えられている [2, 3, 4].
の鞍点となる.また,次のような拡張ラグランジュ関数(augmented Lagrangian function) に基づく双対性も考えられている [2, 3, 4].
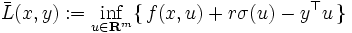 |
ただし,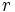 は正定数,
は正定数,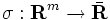 は
は 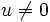 に対して
に対して 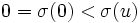 を満足する下半連続な真凸関数である.関数
を満足する下半連続な真凸関数である.関数 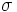 の例としては
の例としては 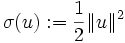 などがある.さらに、最近では大域的最適化(global optimization)や抽象的凸解析(abstract convex analysis)の立場からの研究も行われている[5].
などがある.さらに、最近では大域的最適化(global optimization)や抽象的凸解析(abstract convex analysis)の立場からの研究も行われている[5].
[1] J.M.Borwein and A.S.Lewis, Convex Analysis and Nonlinear Optimization, Theory and Examples(Second Edition), Springer, NewYork, 2006.
[2] 福島雅夫,『非線形最適化の基礎』, 朝倉書店, 2001.
[3] 今野浩, 山下浩,『非線形計画法』, 日科技連, 1978.
[4] R.T. Rockafellar and R. J-B. Wets, Variational Analysis, Springer, Berlin, 1998.
[5] A.M.Rubinov, Abstract Convexity and Global Optimization, Kluwer Academic, Dordrecht, 2000.
- 双対性理論のページへのリンク
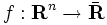
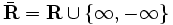 ),
), 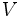 は
は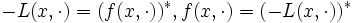 が
が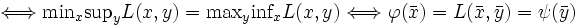
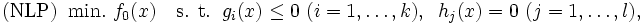
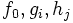 は
は 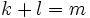 )
)