帰納極限 帰納極限の概要

ウィキペディア

帰納極限

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2023/02/15 08:32 UTC 版)

厳密な定義

代数系の帰納極限

本節では、対象はある決まった代数的構造（例えば群や環あるいは適当に固定された環上の加群や多元環など）をもつ集合とする。このとき準同型は、考えている代数系におけるものを考えることにする。

まず、対象と射（準同型）のなす直系または順系 (direct system) あるいは帰納系 (inductive system) と呼ばれるものの定義から始める。⟨I, ≤⟩ を有向集合とし、{A_i | i ∈ I} を I で添字付けられた対象の族、f_ij: A_i → A_j (i ≤ j) を準同型の族として、以下の条件

1. f_ii は A_i の恒等写像であり、
2. 任意の i ≤ j ≤ k に対して f_ik = f_jk ∘ f_ij が成立する。

が満たされるとき、対、⟨A_i, f_ij⟩ は I 上の帰納系と呼ばれる。

帰納系 ⟨A_i, f_ij⟩ の帰納極限 A の台集合は、A_i の直和集合の適当な同値関係 ∼ による商集合

${\displaystyle \varinjlim A_{i}=\bigsqcup _{i}A_{i}{\bigg /}{\sim }}$

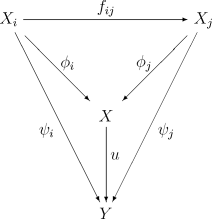
が全ての i, j について可換になる。帰納系 ⟨X_i, f_ij⟩ が既知であるとき、その帰納極限 X はしばしば

${\displaystyle X=\varinjlim X_{i}}$

と書かれる。

前節の場合と異なり、任意の圏においては直極限が存在しないこともありうるが、しかし存在するならば強い意味で一意的である。すなわち、直極限 X と別の直極限 X′ が与えられれば、同型射 X′ → X で全ての標準射と可換になるものが一意的に存在する。

圏 C における直系は、函手の言葉で記述することもできる。任意の半順序集合 ⟨I, ≤⟩ は「i → j ⇔ i ≤ j」として定義される射の集合をもつ小さい圏と見なすことができるから、I 上の直系とは共変函手 I → C に他ならない。

一般の定義

I と C を圏とする。C の固定された対象 X に対して c_X: I → C を定値函手とする。任意の函手 F: I → C に対して、函手

${\displaystyle \varinjlim F\colon C\to \mathbf {Set} }$

を各 X ∈ ob(C) に F から c_X への自然変換の全体のなす集合 Hom(F, c_X) を対応させるものとする。${\displaystyle \varinjlim F}$ が表現可能ならば、C における表現対象を F の直極限と呼び、やはり ${\displaystyle \varinjlim F}$ と書く。

C がアーベル圏ならば任意個（無限個でもよい）の対象の直和が存在する（グロタンディークの公理 AB3）から、${\displaystyle \varinjlim F}$ は任意の函手 F: I → C に対して表現可能であり、

${\displaystyle \varinjlim \colon {\text{Hom}}({\mathcal {I}},{\mathcal {C}})\to {\mathcal {C}};\quad F\mapsto \varinjlim F}$

はアーベル圏の右完全加法的函手である。

例

• A_i を長さiの有限数列全体からなる集合、f_ij (i≤j) を数列の後ろに0をj-i項付け加える写像とすると、その帰納極限は、有限項を除いて0であるような数列全体の集合となる。
• 集合 M の部分集合族 M_i は包含関係によって半順序集合となる。この族が直系となるならば、その帰納極限は単に和集合 ${\displaystyle \bigcup M_{i}}$ によって与えられる。同様のことは、ある群の部分群がなす直系や、ある環の部分環がなす直系についても成立する。
• 添字集合 I が有向集合で最大元 m を持つならば、そのような任意の直系の直極限はX_m に同型であり、標準射 φ_m: X_m → X は同型となる。
• p を素数とすると、群の族 Z/pⁿZ および p を掛けることで誘導される準同型の族 Z/pⁿZ → Z/pⁿ⁺¹Z での組は帰納系を成す。この帰納系の帰納極限は、p の適当な冪を位数とするような 1 の冪根の全体からなる。これをプリューファー群 Z(p^∞) という。
• F を位相空間 X 上の C-値層とする。X の点 x を固定して、x の開近傍の全体は包含関係を逆にする順序によって（つまり U ≤ V ⇔ U ⊇ V とおいて）有向半順序集合を成す。このとき、r を制限写像とする直系 (F(U), r_U,V) が得られ、この系の直極限は x における F の茎 F_x と呼ばれる。x の各近傍 U に対して標準射 F(U) → F_x は F の U 上の切断 s を茎 F_x の元 s_x へ対応させる。元 s_x は切断 s の x における芽と呼ばれる。
• 位相空間の圏における直極限は、台集合に対する単に集合としての直極限を取ったものを台として、終位相を入れたものをいう。
• 直極限と逆極限の間には
  ${\displaystyle \mathrm {Hom} (\varinjlim X_{i},Y)=\varprojlim \mathrm {Hom} (X_{i},Y)}$
  を通じた相互関係がある。
• 列 {A_n, φ_n} で A_n はC*-環、φ_n: A_n → A_n+1 は *-準同型とする。直極限構成の C*-類似は上述の普遍性を満足する C*-環によって与えられる。