射影多様体射影多様体の概要

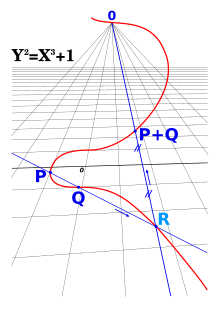
1次元の射影多様体は射影曲線と呼ばれ、2次元だと射影曲面、余次元 1 だと射影超曲面と呼ばれる。射影超曲面は単独の斉次式の零点集合である。

射影多様体 $X$ が斉次素イデアル $I$ によって定義されているとき、商環

k[x_{0},\ldots ,x_{n}]/I

は $X$ の斉次座標環と呼ばれる。次数や次元のような基本的な不変量は、この次数環のヒルベルト多項式から読み取ることができる。

射影多様体は多くの方法で生じる。それらは完備（英語版）であり、荒っぽく言えば「抜けている」点がない。逆は一般には正しくないが、チャウの補題（英語版）はこの2つの概念の近い関係を記述する。多様体が射影的であることは直線束や因子を調べることによって示される。

射影多様体の顕著な性質の1つは、層コホモロジーの有限性である。滑らかな射影多様体に対して、セール双対性はポワンカレ双対性の類似と見なせる。それはまた射影曲線、すなわち次元（英語版） 1 の射影多様体に対するリーマン・ロッホの定理を導く。射影曲線の理論は特に豊かで、曲線の種数（英語版）による分類を含む。高次元の射影多様体の分類問題は自然に射影多様体のモジュライの構成を導く^[1]。ヒルベルトスキームは所定のヒルベルト多項式をもつ $P n$ の閉部分スキームをパラメトライズする。ヒルベルトスキームは、グラスマン多様体は特別な場合であるが、それ自身射影スキームでもある。幾何学的不変式論は別のアプローチを提供する。古典的なアプローチはタイヒミュラー空間や周多様体（英語版）を含む。

古典にさかのぼる特に豊かな理論が、複素射影多様体、すなわち $X$ を定義する多項式が複素係数を持つ場合にある。大まかには、GAGA の原理により、射影複素解析空間（あるいは多様体）の幾何学は射影複素多様体の幾何学と等しい。例えば、 $X$ 上の正則ベクトル束（より一般に連接解析的層）の理論は、代数的ベクトル束の理論と一致する。Chow の定理により、射影空間の部分集合が正則関数の族の零点集合であることと斉次多項式の零点集合であることは同値である。複素射影多様体に対する解析的な手法と代数的な手法の組合せはホッジ理論のような分野に通じる。

脚注

注

^ この斉次イデアルは $I$ の斉次化と呼ばれることがある。
^ この定義は Eisenbud–Harris 2000, III.2.3 とは異なるが、ウィキペディアの他の記事と整合的である。
^ cf. the proof of Hartshorne 1977, Ch II, Theorem 7.1
^ これは難しくない(Hartshorne 1977, Ch III. Lemma 2.10)： ${\mathcal {F}}$ の脆弱分解（英語版）とその射影空間全体への零拡張を考える。
^ To make the construction work, one needs to allow for a non-variety.

出典

^ Kollár & Moduli, Ch. I.
^ Shafarevich, Igor R. (1994), Basic Algebraic Geometry 1: Varieties in Projective Space, Springer
^ Mumford 1999, p. 82.
^ Hartshorne 1977, Section II.5.
^ Mumford 1999, p. 111.
^ Grothendieck & Dieudonné 1961, 5.6.
^ Hartshorne 1977, Ch II. Exercise 4.5.
^ Humphreys, James (1981), Linear algebraic groups, Springer , Theorem 21.3.
^ Hartshorne, Ch. V, Exercise 3.4. (e)..
^ Fulton 1998, Proposition 8.4..
^ Hartshorne, Ch. II, Exercise 5.14. (a).
^ Rosen, Michael (2002), Number theory in Function Fields, Springer
^ Hartshorne, 1977 & Ch IV, Exercise 1.7.
^ Hartshorne 1977, Ch I, Exercise 2.8; その理由は、{{Pⁿ}} の斉次座標環は一意分解整域であって、そのような環では高さ 1 の任意の素イデアルは単項イデアルだからである。
^ Shafarevich 1994, Ch. I. § 4.4. Example 1..
^ Mumford, Ch. II, § 7. Proposition 6..
^ Hartshorne, Ch. I, Exercise 4.9..
^ Hartshorne 1977, Ch II, Theorem 7.1.
^ Hartshorne 1977, Ch II, Proposition 7.2.
^ Hartshorne 1977, Ch III. Theorem 5.2.
^ Hartshorne 1977, Ch III. Exercise 5.2.
^ Hartshorne 1977, Ch IV. Theorem 1.3.
^ Kollár 1996, Ch. I 1.4.
^ Eisenbud & Harris 2000, VI 2.2
^ Hartshorne 1977, Appendix B. Theorem 3.4..
^ Griffiths-Adams, IV. 1. 10. Corollary H.
^ Griffiths-Adams, IV. 1. 10. Corollary I.
^ Hartshorne 1977, Appendix B. Theorem 2.1.
^ Mumford 1970, p. 36.
^ Hartshorne 1977, Ch III. Remark 7.15..
^ Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, Birkhäuser
^ Dolgachev, Igor (1982), “Weighted projective varieties”, Group actions and vector fields (Vancouver, B.C., 1981), Lecture Notes in Math., 956, Berlin: Springer, pp. 34–71, doi:10.1007/BFb0101508, MR 0704986

[前の解説]

[続きの解説]

「射影多様体」の続きの解説一覧

[3] この斉次イデアルは $I$ の斉次化と呼ばれることがある。

[7] この定義は Eisenbud–Harris 2000, III.2.3 とは異なるが、ウィキペディアの他の記事と整合的である。

[8] . the proof of Hartshorne 1977, Ch II, Theorem 7.1

[23] これは難しくない(Hartshorne 1977, Ch III. Lemma 2.10)： ${\mathcal {F}}$ の脆弱分解（英語版）とその射影空間全体への零拡張を考える。

[28] To make the construction work, one needs to allow for a non-variety.

[FOOTNOTEKollárModuliCh._I-1] Kollár & Moduli, Ch. I.

[2] Shafarevich, Igor R. (1994), Basic Algebraic Geometry 1: Varieties in Projective Space, Springer

[FOOTNOTEMumford199982-4] Mumford 1999, p. 82.

[FOOTNOTEHartshorne1977Section_II.5-5] Hartshorne 1977, Section II.5.

[FOOTNOTEMumford1999111-6] Mumford 1999, p. 111.

[FOOTNOTEGrothendieckDieudonné19615.6-9] Grothendieck & Dieudonné 1961, 5.6.

[FOOTNOTEHartshorne1977Ch_II._Exercise_4.5-10] Hartshorne 1977, Ch II. Exercise 4.5.

[11] Humphreys, James (1981), Linear algebraic groups, Springer , Theorem 21.3.

[FOOTNOTEHartshorneCh._V,_Exercise_3.4._(e).-12] Hartshorne, Ch. V, Exercise 3.4. (e)..

[FOOTNOTEFulton1998Proposition_8.4.-13] Fulton 1998, Proposition 8.4..

[FOOTNOTEHartshorneCh._II,_Exercise_5.14._(a)-14] Hartshorne, Ch. II, Exercise 5.14. (a).

[15] Rosen, Michael (2002), Number theory in Function Fields, Springer

[FOOTNOTEHartshorne1977Ch_IV,_Exercise_1.7.-16] Hartshorne, 1977 & Ch IV, Exercise 1.7.

[17] Hartshorne 1977, Ch I, Exercise 2.8; その理由は、{{Pⁿ}} の斉次座標環は一意分解整域であって、そのような環では高さ 1 の任意の素イデアルは単項イデアルだからである。

[FOOTNOTEShafarevich1994Ch._I._§_4.4._Example_1.-18] Shafarevich 1994, Ch. I. § 4.4. Example 1..

[FOOTNOTEMumfordCh._II,_§_7._Proposition_6.-19] Mumford, Ch. II, § 7. Proposition 6..

[FOOTNOTEHartshorneCh._I,_Exercise_4.9.-20] Hartshorne, Ch. I, Exercise 4.9..

[FOOTNOTEHartshorne1977Ch_II,_Theorem_7.1-21] Hartshorne 1977, Ch II, Theorem 7.1.

[FOOTNOTEHartshorne1977Ch_II,_Proposition_7.2-22] Hartshorne 1977, Ch II, Proposition 7.2.

[FOOTNOTEHartshorne1977Ch_III._Theorem_5.2-24] Hartshorne 1977, Ch III. Theorem 5.2.

[FOOTNOTEHartshorne1977Ch_III._Exercise_5.2-25] Hartshorne 1977, Ch III. Exercise 5.2.

[FOOTNOTEHartshorne1977Ch_IV._Theorem_1.3-26] Hartshorne 1977, Ch IV. Theorem 1.3.

[FOOTNOTEKollár1996Ch._I_1.4-27] Kollár 1996, Ch. I 1.4.

[29] Eisenbud & Harris 2000, VI 2.2

[FOOTNOTEHartshorne1977Appendix_B._Theorem_3.4.-30] Hartshorne 1977, Appendix B. Theorem 3.4..

[FOOTNOTEGriffiths-AdamsIV._1._10._Corollary_H-31] Griffiths-Adams, IV. 1. 10. Corollary H.

[FOOTNOTEGriffiths-AdamsIV._1._10._Corollary_I-32] Griffiths-Adams, IV. 1. 10. Corollary I.

[FOOTNOTEHartshorne1977Appendix_B._Theorem_2.1-33] Hartshorne 1977, Appendix B. Theorem 2.1.

[FOOTNOTEMumford197036-34] Mumford 1970, p. 36.

[FOOTNOTEHartshorne1977Ch_III._Remark_7.15.-35] Hartshorne 1977, Ch III. Remark 7.15..

[36] Esnault, Hélène; Viehweg, Eckart (1992), Lectures on vanishing theorems, Birkhäuser

[37] Dolgachev, Igor (1982), “Weighted projective varieties”, Group actions and vector fields (Vancouver, B.C., 1981), Lecture Notes in Math., 956, Berlin: Springer, pp. 34–71, doi:10.1007/BFb0101508, MR 0704986

[1]

射影多様体 射影多様体の概要

射影多様体

注

出典

急上昇のことば

「射影多様体」の関連用語

射影多様体射影多様体の概要