ベイズの定理

統計学用語辞典

ベイズの定理

　2 つの事象 A，B があるとき，
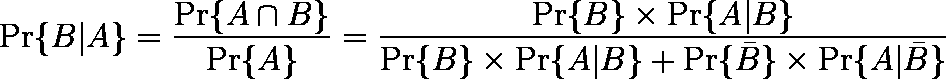
を ベイズの定理 という。
　一般的には，B が r 個の排反事象に分かれるとき，観察された事象 A の原因が Bi である確率は，
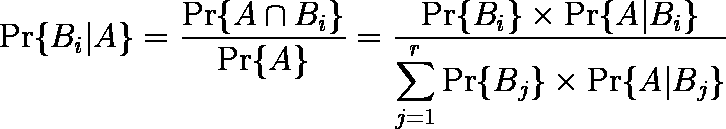
となる。Pr｛Bi｝ は 事前確率，Pr｛Bi | A｝ は 事後確率 と呼ばれる。
　例えば，A が女性であること，Bi が学年（ i = 1,2,3,4 ）としたとき，Pr｛Bi | A｝ は，ランダムに抽出した学生が女子学生であるとわかったとき，その学生が Bi 学年である確率を表す。

表 1．ベイズの定理の導き方

学年	男子	女子	合計	女子の割合		学年の割合	ベイズ確率
				Pr｛A | Bi｝	Pr｛Bi∩A｝	Pr｛Bi｝	Pr｛Bi | A｝
B1	90	36	126	36/126	36/510	126/510	0.2209
B2	76	45	121	45/121	45/510	121/510	0.2761
B3	87	43	130	43/130	43/510	130/510	0.2638
B4	94	39	133	39/133	39/510	133/510	0.2393
合計	347	163	510	Pr｛A｝=163/510

　事前にわかっている確率は Pr｛Bi｝， Pr｛A | Bi｝ だけでよい。
　事後にわかった事実 “女子である” ということから，事後確率 Pr｛Bi | A｝ を得ようとするのが問題の趣旨である。
　2 年生の女子である確率 Pr｛B2 ∩ A｝ = 45 / 510 は，2 年生である確率 Pr｛B2｝ = 121 / 510 と 2 年生であるという条件付きでの女子である確率 Pr｛A | B2｝ = 45 / 121 を用いて乗法定理の ( 2 ) 式から，
　　Pr｛B2 ∩ A｝
　　= Pr｛B2｝ ・ Pr｛A | B2｝
　　= 121 / 510 ・ 45 / 121
　　= 45 / 510　　…… ( 4 )
である。
　女子であるという条件付きでの 2 年生である確率 Pr｛B2 | A｝ は，乗法定理の ( 1 ) 式から，
　　Pr｛B2 | A｝= Pr｛B2 ∩ A｝/ Pr｛A｝
であり，（ 4 ）式および，
　　Pr｛A｝
　　= Pr｛B1 ∩ A｝ + Pr｛B2 ∩ A｝ + Pr｛B3 ∩ A｝ + Pr｛B4 ∩ A｝
　　= 36 / 510 + 45 / 510 + 43 / 510 + 39 / 510
　　= 163 / 510
であるから，
　　Pr｛B2 | A｝
　　= （ Pr｛B2｝ ・ Pr｛A | B2｝）/ Pr｛A｝
　　= （121 / 510 ・ 45 / 121）/（163 / 510）
　　= 0.2761
となる。