動的計画
【英】:dynamic programming
概要
1957年, ベルマン (R.E. Bellman) によって提案された多変数最適化問題を解くための手法. 目的関数に再帰性(可分性)と単調性があり, 制約式が逐次的であるとき, 原問題をある部分問題群に埋め込んで, 各部分問題の最適値を定義し, 相隣る問題の最適値間の関係式(再帰式)を導く. これを逐次解いて, 最後に与問題の最適解を求める方法である. 解法の効率化のためには, 決定変数, 状態変数, 評価関数などの選択・設定に個々の創意工夫を要する.
詳説
多変数最適化問題の目的関数が再帰性(可分性)と単調性をもち, 制約条件に逐次性があるとき, 再帰式 を導いて, これを1変数ずつ解いて最後に与問題の最適解を求めようとする方法を, 動的計画(dynamic programming)と呼ぶ. 原理としては 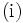 最適性の原理 (principle of optimality),
最適性の原理 (principle of optimality), 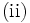 不変埋没原理(principle of invariant imbedding),
不変埋没原理(principle of invariant imbedding), 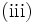 因果律の原理(principle of causality), の三つに基づく[1]. 最適性の原理には
因果律の原理(principle of causality), の三つに基づく[1]. 最適性の原理には  オリジナル版,
オリジナル版,  シンプル版,
シンプル版,  "
" "版,
"版,  構造解析版,
構造解析版,  数学版, などがある[9]. 数学的にはマックスマックス定理 に遡ることができる[2][4]. 応用面では, 逐次決定過程 [3][6]の基本原理として用いられ, マルコフ決定過程の政策改良法, 最短経路問題のダイクストラ法, 巡回セールスマン問題など種々の最適化問題の解法としてアルゴリズムに組み込まれている.
数学版, などがある[9]. 数学的にはマックスマックス定理 に遡ることができる[2][4]. 応用面では, 逐次決定過程 [3][6]の基本原理として用いられ, マルコフ決定過程の政策改良法, 最短経路問題のダイクストラ法, 巡回セールスマン問題など種々の最適化問題の解法としてアルゴリズムに組み込まれている.


で定義する. 構成要素の1変数関数  がすべて単調な(狭義単調な)とき, 特に単調性(狭義単調性)をもつ再帰型関数という. 単調性をもつ再帰型関数
がすべて単調な(狭義単調な)とき, 特に単調性(狭義単調性)をもつ再帰型関数という. 単調性をもつ再帰型関数  を目的式と制約式にする主問題
を目的式と制約式にする主問題


に埋め込み, この最大値を  とする. このとき, 制約式の狭義単調性と両式の連続性を仮定すると, 再帰式
とする. このとき, 制約式の狭義単調性と両式の連続性を仮定すると, 再帰式
 |
 |
が成り立つ. ただし,  は
は  の逆関数. この再帰式を後向きに解いて, 最後に主問題の最大値
の逆関数. この再帰式を後向きに解いて, 最後に主問題の最大値  が得られる. これが動的計画法である. さらに, 主問題
が得られる. これが動的計画法である. さらに, 主問題  と逆問題
と逆問題

の解(最小値関数と最小点関数)の間には互いに逆関数の関係にある(逆定理 [5]). これは線形計画における双対定理に類似して, 動的計画の双対定理と考えられる[11].

で表わされる. これに対して反転関数(逐次パラメトリック逆関数)  を
を

で定義する. このとき, 目的式 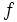 , 制約式
, 制約式 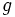 (ただし
(ただし  をもつ主問題の反転問題を
をもつ主問題の反転問題を

で考えると, 反転問題の最小値は主問題の終端値となる (反転定理 [7]).
さらに, 準線形化, 最大変換(共役変換)による双対理論を組み込んだ三面鏡理論 [8]が制御過程上で展開されている. 逆問題, 反転問題, 双対問題は基本的に動的計画法で解くことができるが, それぞれの問題の最適解は直接解くことなく, 対応する定理によって得られる[7].
再帰性, 単調性がない場合の最適化としては, 非可分性との関連で結合性などの下で事前条件付き決定過程, 事後条件付き決定過程[10]がファジィ動的計画, 非加法型再帰的効用関数の経済学などで研究されている. これらの問題はマルコフ政策のクラスで再帰式が導かれる.
[1] R. Bellman, Dynamic Programming, Princeton Univ. Press, 1957.
[2] G. H. Hardy, J. E. littlewood and G. Pólya, Inequalities, 2nd ed., Cambridge Univ. Press, 1952.
[3] 茨木俊秀,『組合せ最適化の理論』, 電子通信学会, 1979.
[4] 伊理正夫ほか, 座談会「最大問題最小問題をめぐって」,『数学セミナー』, 7月号 (1966), 40-48.
[5] S. Iwamoto, "Inverse Theorems in Dynamic Programming I, II, III," Journal of Mathematical Analysis and Applications, 58 (1977), 113-134, 249-279, 439-448.
[6] 岩本誠一,「逐次決定過程としての動的計画論I,II」,『オペレーションズ・リサーチ』, 22 (1977), 427-434, 496-501.
[7] 岩本誠一,『動的計画論』, 九州大学出版会(経済工学シリーズ), 1987.
[8] S. Iwamoto, "A three mirror problem on dynamic programming," in Proceedings of the Third Bellman Continuum Workshop, 363-382, 1989.
[9] 岩本誠一,「動的計画の最近の進歩」, 第2回RAMPシンポジウム論文集, 129-140, 1990.
[10] S. Iwamoto, "Conditional decision processes with recursive reward function,"Journal of Mathematical Analysis and Applications, 230 (1999), 193-210.
- 動的計画のページへのリンク
 は
は  を
を 
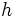 が
が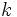 をもつときは
をもつときは 