Perron-Frobenius定理
【英】:Perron-Frobenius theorem
フロベニウス(Frobenius)により明らかにされた非負行列の固有値の諸性質は 数多くのフロベニウス定理として広く知られている. その中で,ペロン-フロベニウス(Perron-Frobenius)定理は非負行列の絶対値 最大固有値の上下限を最適化問題の最適値として与えるものである. 本定理はそもそもペロンが正行列に対して証明した内容をフロベニウスが 非負行列にまで拡張したものであり,その定理は以下の通りである.
非負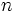 次正方行列
次正方行列![[a_{ij}]](https://cdn.weblio.jp/e7/img/dict/orjtn/58f102d707b5918d8445e64dc0e6db1f.png) は既約とする.
行列
は既約とする.
行列![[a_{ij}]](https://cdn.weblio.jp/e7/img/dict/orjtn/58f102d707b5918d8445e64dc0e6db1f.png) の絶対値最大固有値
の絶対値最大固有値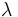 は
は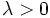 であり,
であり,
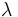 に対応する固有ベクトル
に対応する固有ベクトル![[z_1,\ldots,z_n]^{\top}](https://cdn.weblio.jp/e7/img/dict/orjtn/05d574ca6d1603aab761df15fe8c3704.png) はスカラー倍を除いて一意である.
ここで,
はスカラー倍を除いて一意である.
ここで,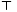 は転置を示す.さらに,
成分が全て正である任意の
は転置を示す.さらに,
成分が全て正である任意の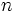 次元ベクトル
次元ベクトル
![[x_1,\ldots,x_n]^{\top}](https://cdn.weblio.jp/e7/img/dict/orjtn/bd9559aec10885a1a6650d395e29e7d5.png) に対して,
に対して,
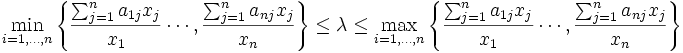
|
が成立し,
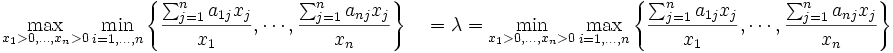
|
- Perron-Frobenius定理のページへのリンク
![[x_1,\cdots,x_n]^{\top}](https://cdn.weblio.jp/e7/img/dict/orjtn/d2e1ac0a5a0ddda424140f80264dcda9.png)
