展開形ゲームとは - OR事典 Weblio辞書

Weblio 辞書 > 同じ種類の言葉 > 文化 > 娯楽 > ゲーム > 展開形ゲームの意味・解説

OR事典

展開形ゲーム

読み方：てんかいけいげーむ
【英】：game in extensive form

概要

プレイヤーの手番の系列をグラフ理論の有向木を用いて表現するゲームのモデル. 木の分岐点はプレイヤーの手番, 枝はプレイヤーの選択肢または行動を表す. ゲームのプレイは木の初期点から始まり木の1つの終点に到達して終了する. プレイヤーの同時的な意思決定を定式化する戦略形ゲームに対して, 展開形ゲームはプレイヤーの動学的な意思決定問題を分析するために用いられる.代表的な均衡概念に部分ゲーム完全均衡, 完全均衡や逐次均衡がある.

詳説

展開形ゲーム (game in extensive form) はプレイヤーの手番の系列をゲームの木 (game tree) を用いて表現するモデルである. ゲームの木 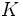$K\,$ はグラフ理論でいう有向木で, 木の分岐点はプレイヤーが選択肢を選ぶ手番, 枝はプレイヤーの選択肢あるいは行動を表す. 木の始点から終点までの経路をゲームの1つのプレイという.

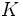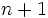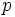プレイヤー分割 $P=[P_{0}, P_{1}. \cdots, P_{n}]\,$ は, ゲームの木 $K\,$ の分岐点の全体を $n+1\,$ 個の部分集合に分割する. $P_{i}\ (i=1, 2, \cdots, n)\,$ はプレイヤー $i\,$ の手番の集合を表す. $P_{0}\,$ に含まれる手番は偶然手番とよばれ, プレイヤーの意思とは無関係な偶然機構によって枝が選択される. 天候やトランプゲームでランダムにカードを配るなどは, 偶然手番の典型的な例である. 偶然手番に対しては枝の選択を行なう確率分布 $p\,$ が付与される.

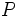ゲームの情報分割 $U=[U_{0}, U_{1}, \cdots, U_{n}]\,$ は,プレイヤー分割 $P\,$ の細分割である.各 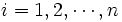$i=1, 2, \cdots, n\,$ に対して $U_{i}=[u_{i1}, u_{i2}, \cdots, u_{im_{i}}]\,$ はプレイヤー $i\,$ の手番の集合 $P_{i}\,$ を $m_{i}\,$ 個の非空な部分集合に分割する. $U_{i}\,$ に属する部分集合 $u_{ij}\ (j=1, 2, \cdots, m_{i})\,$ をプレイヤー $i\,$ の情報集合 (information set) という.プレイヤーは行動を選択するとき,自分の手番がどの情報集合に属するかは知っているが,情報集合の中のどの分岐点であるかは知らない.

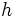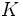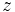ゲームの利得関数 $h\,$ は,ゲームの木 $K\,$ の各終点 $z\,$ に対してプレイヤーの利得ベクトル $h(z)=(h_{1}(z), h_{2}(z), \cdots, h_{n}(z))\,$ を対応させる.

形式的には, 展開形ゲーム 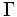$\Gamma\,$ は以上の5つの要素の組 $(K, P, p, U, h)\,$ によって定義される. これらの5つの構成要素をゲームのルールという.

図１：展開形ゲーム

展開形ゲームの例として図1を考える.プレイヤー1と2の情報分割はそれぞれ $U_{1}=[u_{1}], U_{2}=[u_{21}, u_{22}]\,$ である.図1では最初にプレイヤー1がRとLの2つの行動のうち1つを選択する. 次に, プレイヤー2はプレイヤー1の選択を知った上で, RとLのうちから1つの行動を選択する.ゲームは4つの終点をもち, 終点に付与されている利得ベクトルは上の数字がプレイヤー1の利得, 下の数字がプレイヤー2の利得を表す.

図1のゲームのように, プレイヤーのすべての情報集合がただ1つの分岐点から成るゲームを完全情報ゲーム (game with perfect information) といい, そうでないゲームを不完全情報ゲーム (game with imperfect information) という. 完全情報ゲームでは, すべての手番においてプレイヤーはゲームの過去のプレイの経過を完全に知った上で行動を選択できる. チェスや将棋は完全情報ゲームである.

展開形ゲームの部分木でそれ自身が展開形ゲームの構造をもつものを部分ゲームという. 図1のゲームは, 情報集合 $u_{21}\,$ と $u_{22}\,$ から始まる2つの部分ゲームをもつ.

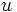プレイヤー $i\,$ の各情報集合 $u\in U_{1}\,$ に対して $u\,$ における選択肢の集合上の 1つの確率分布 $b_{i}(u)\,$ を対応させる関数 $b_{i}\,$ をプレイヤー $i\,$ の行動戦略 (behavior strategy) という. 特に, すべての情報集合に対して 1つの選択肢を確定的に対応させる行動戦略を純戦略という.

例えば, 図1のゲームにおいて, プレイヤー1の純戦略 $\pi_{1}\,$ はRとLの2通りであり, プレイヤー2の純戦略 $\pi_{2}\,$ は, RR, RL, LR, LLの4通りである. ただし, 前の文字は情報集合 $u_{21}\,$ でとる行動, 後の文字は情報集合 $u_{22}\,$ でとる行動を表す. 図1の展開形ゲームから, プレイヤーの純戦略と利得の関係によって図2のような戦略形ゲームを作ることができる.

1, 1*

-2, 0

-1, 0

0, 1

-1, 0

0, 1*

図2：図1の展開形ゲームから作られた戦略形ゲーム

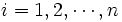プレイヤーの行動分析のための最も基本的なゲームの解の概念は, ナッシュ (J. F. Nash) によって定義された非協力均衡点である. 一般にナッシュ均衡と呼ばれている. 展開形ゲームの行動戦略の組 $b^{*}=(b_{1}^{*}, b_{2}^{*}, \cdots, b_{n}^{*})\,$ がナッシュ均衡であるとは,すべてのプレイヤー $i=1, 2, \cdots, n\,$ のすべての行動戦略 $b_{i}\,$ に対して,

$H_{i}(b^{*}) \ge H_{i}(b^{*}/b_{i})\,$

が成り立つことである. ただし, $b^{*}/b_{i}\,$ は $b^{*}\,$ からプレイヤー $i\,$ だけが戦略を $b_{i}^{*}\,$ から $b_{i}\,$ に変更してできる行動戦略の組を表し, $H_{i}\,$ はプレイヤー i の期待利得関数を表す.

完全情報ゲームのナッシュ均衡は, 最初に, 終点に一番近い分岐点で, その手番のプレイヤーの利得を最大にする最適戦略を求め, 以下順次, ゲームの木を後向きに解くことによって計算できる. 例えば, 図1のゲームで情報集合 $u_{21}\,$ と $u_{22}\,$ におけるプレイヤー2の最適戦略はそれぞれLとRである. このとき, 情報集合 $u_{1}\,$ におけるプレイヤー1の最適戦略はRであり, 純戦略の組 (R, LR) はゲームのナッシュ均衡である. このようなナッシュ均衡の計算方法を, ゲームの後向き帰納法という. キューン (H. Kuhn) は, $n\,$ 人完全情報ゲームは純戦略の範囲で少なくとも1つのナッシュ均衡をもつことを証明した [1].

図1のゲームは (R, LR) の他に図2の利得行列で＊をつけたナッシュ均衡をもつ. しかし, これらのナッシュ均衡は均衡プレイ上にない分岐点ではプレイヤーの最適戦略を導かないという欠点をもつ. ゼルテン (R. Selten) はナッシュ均衡のこのような欠点を解消するために, より強い均衡概念として, すべての部分ゲーム上にナッシュ均衡を導く部分ゲーム完全均衡 (subgame perfect equilibrium) を定義した [3].

ゼルテンの研究以後, 展開形ゲームの理論は大きく進展し, 現在, ゲーム的状況におけるプレイヤーの戦略的行動を解明する基礎理論としてORや経済学を始め広範囲の分野に応用されている.

展開形ゲームについて詳しくは, [2] を参照されたい.

参考文献

[1] H. W. Kuhn, "Extensive Games and the Problem of Information," in H. W. Kuhn and A. Tucker(eds.), Contributions to the Theory of Games, Vol. II, Annals of Mathematics Studies 28, Princeton University Press, 1953, 193-216.

[2] 岡田章, 『ゲーム理論』, 有斐閣, 1996.

[3] R. Selten, "Reexamination of the Perfectness Concept for Equilibrium Points in Extensive Games," International Journal of Game Theory, 4 (1975), 25-55.

「OR事典」の他の用語

ゲーム理論：

完全均衡完全情報ゲーム実験展開形ゲーム市場ゲーム微分ゲーム情報集合

索引トップ用語の索引ランキングカテゴリー

展開形ゲームと同じ種類の言葉

>>同じ種類の言葉 >>娯楽に関連する言葉

展開形ゲームに関係した商品

【送料無料】ゲーム理論楽天ブックス
【送料無料】ゲーム理論人間と社会の複雑な関係を解くワードマップ / 佐藤嘉倫【単行本】HMV ローソンホットステーション R
【送料無料】 EXCELで学ぶゲーム理論 / 中野明【単行本】HMV ローソンホットステーション R

>> 「展開形ゲーム」を解説文に含む用語の一覧

>> 「展開形ゲーム」を含む用語の索引

展開形ゲームのページへのリンク

展開形ゲームのページの著作権
Weblio 辞書情報提供元は参加元一覧にて確認できます。

1		井上和子
2		シグナルペプチド
3		井上和子 (女優)
4		沓名環希
5		井上和子_(女優)
6		イノウエカズコ
7		行列のできる法律相談所
8		クルーゾン症候群
9		同居人カップルの殺人推理旅行
10		メガゾーン２３　PARTⅡ　秘密く・だ・さ・い

11		TPP
12		井上和子 (言語学者)
13		出不精
14		捗る
15		先負
16		奇跡の人
17		石松千恵美
18		ハクビシン
19		リーガル・ハイ
20		自由民主党幹事長

21		福利厚生
22		アセスメント
23		タカラダニ
24		未満
25		土曜ワイド劇場
26		言葉
27		ご指導ご鞭撻
28		セクシー・サイン　好き好き好き
29		ダイバーシティ
30		女優


	Copyright (C) 2012 （社）日本オペレーションズ・リサーチ学会 All rights reserved.

展開形ゲームとは？

OR事典

展開形ゲーム

概要

詳説