よう‐りょく〔ヤウ‐〕【揚力】
【揚力】(ようりょく)
揚力
走行中のクルマに上向きに働く空気力をいう。走行中のクルマには、車体上下面の空気流の差によって圧力差が生じ、クルマを持ち上げる方向の力が生じる。前輪揚力の増加は、高速走行中の手応えを減じ、応答性を低下させ、後輪揚力の増加は接地力の減少に伴う安定性の低下を招くため、一般に悪影響がある。また揚力が車高を上げてサスペンションジオメトリーやアライメントを変え、操縦安定性に影響する。低減には車体上面の凹凸を減らして上下面の流速差を低減し、ハッチバックの後端を角張らせ、気流を剥離させて後流の発生を抑えることなどが有効とされる。スポイラーの装着により、ダウンフォースを得ることも可能である。揚力を動圧と前面投影面積で除した値を揚力係数といい、揚力の派生しやすさを示す。
参照 ピッチングモーメント揚力
物体を持ち上げようとする空気力。走行中の車体に空気が下から潜り込んで持ち上げるような作用をする。速い気流のもとでは車体が吸い上げられる。ごくわずかな力だが、これらが揚力として作用する。その結果、車両はハンドルが効きにくくなり安定性が失われる。つまり、揚力は小さいほどその車体デザインは優れている。記号はL。揚力の大小を示す揚力係数はCLで示される。風洞内の天秤ではかるときは、前輪と後輪で区別してはかり、前輪の揚力係数はCLf、後輪の揚力係数はCLRで表す。
揚力(ようりょく)
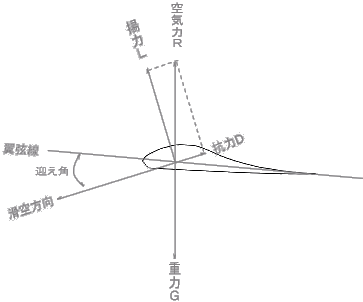 |
| 揚力についてのベクトル |
なぜ揚力が発生するか?はベルヌイの定理を参照。
★揚力と抗力から合成された力、空気力(R)と重力とつり合い、バラグライダーは滑空している。
★翼弦線は水平線ではなく、翼の方向である。
★迎え角とは滑空方向に対する翼の上向きの角度であることが判る。
★揚力は滑空方向に対し直角に発生している。
★抗力が減っていくと揚力のベクトルは空気力に近づき、仮に抗力がゼロになると滑空方向は水平となる。
★揚力と抗力の比、揚抗比は滑空比と等しくなる。
揚力は次のような式で求められる。
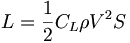 注意
注意 ★この式から揚力(L)は速度の2乗に比例している事が判るが、
無動力で飛行するパラグライダーにおいて、例えばアクセルなどを利用してスピードを増した場合、
アクセルにより迎え角が小さくなり揚力係数がそれに比例して小さくなる。
従って揚力が増大することはない。
★揚力(L)は飛行時には近似値として総重量(G)と吊りあっている。
この公式を利用してバラストなどで重量を増した場合、どの位スピードが増すか?また同じ機種のグライダーでサイズを小さくすると、どの位スピードが増すか?など調べて見るのもおもしろい。
揚力
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/08/22 08:07 UTC 版)

|
揚力(ようりょく、英語: lift)は、流体(液体や気体)中を移動もしくは流れにさらされた物体が、流体から受ける力(流体力)の成分の一つで、物体の進行方向や流れが物体に向かう方向に対して垂直に働く力を指す。一方、進行方向に平行する成分は抗力と呼ぶ。そしてこの揚力と抗力の比を揚抗比と呼ぶ。
通常、物体と流体に相対速度があるときに発生する力(動的揚力)のみを指し、物体が静止していてもはたらく力である浮力(静的揚力)は含まない。
揚力の応用例として、重力と反対方向へ揚力を生じさせることで飛行機の巡航時に垂直方向の釣り合いをとる
概要

空気や水といった流体の中に物体があり、物体とその周囲の流体との間に相対速度がある時、物体とともに移動する視点について「主流」および「主流速度」が定義できる。このとき、その物体は流体との接触面を介して周囲流体と力を及ぼし合う。すなわち物体から受ける力によって周囲の流れは変化し、同時に物体は流れから力を受ける。
物体が主流方向に受ける力を抗力とよぶ。
物体が主流速度ベクトルに対して対称な形状である場合、主流に垂直な力の成分は生じないが、非対称な形状の場合は、物体は主流方向からそれた斜めの方向に力を受け、主流に垂直な力の成分を揚力とよぶ。
- それ自体の形状が上下対称であっても(正の)迎角がある場合は、主流に対して非対称であり、揚力を発生する。例えば、単純な平板の形状・上下対称の翼型がある。→凧や帆
- カルマン渦と揚力
- 物体後流にはカルマン渦と呼ばれる渦列が周期的に発生し、流体力は振動していることが多い。このため、回転なし迎角なしで正味の揚力がゼロとされる形状であっても瞬時の揚力は生じている事がある。
- 翼表面上の圧力
- 流体が物体におよぼす力は、物体表面の応力、すなわち圧力と摩擦を表面すべてで積算した量である。ただし、揚力は圧力だけで説明できると考えられており、圧力場を物体表面で積算した合力が揚力である。したがって揚力が上向きのときに物体表面の圧力分布をみると物体上側で低圧、下側で高圧の傾向がある。
- 速度場
- 翼表面圧力が上部で低圧である以上、対応する速度をみると物体の上側で高速下側で低速の分布である。このため翼型境界線で循環を見積もると有限の値をとる。
- また、物体に揚力が働いているとき、揚力に対する反作用として揚力と逆向きの運動が物体周囲の流体のどこかにかならず生じる。翼体の上背面から翼後端の後方にかけて顕著な下向きの流れは、主に航空機工学の分野において「ダウンウォッシュ」と呼ばれる。
- 翼まわりの渦
- ダウンウォッシュは翼後縁が横切った矩形状領域に生じる。この矩形状の線は下降流と上昇流の境であり、せん断すなわち渦度が集中し、渦が生じる。ただし矩形の前方側は翼体によって仕切られているため翼まわりの循環が渦の代わりとなる。ダウンウォッシュは翼後縁と2つの翼端渦と出発渦とで囲まれた形となる。
- ダウンフォース
- 「揚力」は字義どおりに重力の反対方向に働くとは限らない。飛行機の場合、機体の姿勢に合わせて機体からみた上方向に働く力を揚力とする。レーシングカー等では下向き揚力をダウンフォースと呼び表すことがある。帆船の帆に働く揚力はほぼ水平方向を向いている。風車やタービンでは周方向、プロペラでは回転軸方向がおおよその揚力の向きとなる。
- 揚力を利用する例
- 揚力の利用例として、植物の種子、昆虫の翅、水性動物のヒレ、鳥類の翼、凧、飛行機の固定翼、ヘリコプターの回転翼、水中翼船の水中翼、船舶の帆(縦翼)と舵、櫂、プロペラ、ファン、タービンなどがある。
上記の図のように、流線の密度が疎な部分には、カルマン渦に代表される渦の形成が容易になる[要出典]、これは時間的周期性を持ち円柱断面を仮定した場合上にも下にも揚力を形成し、流体関連振動となる。この原因は渦の離脱による圧力低下が原因であり、それを非対称に設計したジューコフスキー的形状においてはカルマン渦の発生が上下非対称になるため揚力が発生する。そのため、そういう周期的圧力欠損に頼るため、小さな航空機では振動が激しくなる[要出典]。
揚力の式
物体に働く揚力は正味の動圧とそれが作用する面積に依存した量と考えられるため、一般に以下の式で表される。
-


翼型
翼型とは翼の断面形状のこと。詳しくは「翼型」を参照。
基本的には、前端側が丸く後端側が尖ったいわゆる「涙滴形」やそれを湾曲させひずませた形状である。航空機の場合は翼内部ボリュームを大きくすることも要求され、翼型設計に影響する。
運用時の迎え角が一定でないことを前提に、前縁部近傍は剥離を防ぐために丸く、曲率を小さくする。翼下面の流れが後端部で翼から離れるために後端は曲率を大きく、尖らせる。
翼断面の図としてよく見られる形状とは、右図上のような形状である。上面側のほうが翼が膨らんでおり、下面側はやや平らになっている。
初期の飛行機は、右下図のような湾曲した形状が用いられた。このような形状では翼下面気流は前縁部を避けた後にさらに後端部をよけることになり、抗力は大きい。1960年代以降広く採用されているスーパークリティカル翼は、低抗力と湾曲とを両立させている。
超音速用途では前端も尖らせた形状が普通である。
翼と迎角
航空機の翼は迎角をつけて機体に固定されている場合が多く、機体が水平でも最低限の揚力を発生する。多くの旅客機の設計では、さらに巡航中は必要な揚力を確保するために機体も1〜2度上向きに傾ける(ただし抗力は僅かに増大する)。
より揚力が必要な状態(低速時、上昇時)では、機体をさらに大きく上向きへ傾ける必要がある。離着陸時にはフラップでさらに揚力を増やす。
プロペラ
一方、プロペラ機のプロペラにも同様のことが成り立つが、翼とは事情が異なる。可変ピッチ機構を持つプロペラの場合は、離着陸時や最高速度域ではピッチ、つまり回転方向に対する迎角を小さくし、一方でプロペラの回転数を上げる。ピッチ角を小さくし抗力を小さくして、プロペラの能率を最大限に高めるためである。一方で巡航時にはピッチ角を大きく取り、エンジンの回転数を下げる。プロペラそれ自体の効率を考えれば抗力が大きくなる分悪化するものの、エンジンの回転数を下げることにより燃費効率が上がる効果のほうがより大きいからである。
マルチローターでないヘリコプターにおいては、ローター(回転翼)の角度調整は極めて重要である。ヘリコプターが前進する時、回転するローターブレードの片方は機体と同じ方向に回転し大気との相対速度が大きく、もう片方は機体と逆方向に回転するため相対速度が小さい。よってローターブレードの左右で揚力の差が生じる。よって回転軸固定のシングルローターヘリコプターには左右のローターブレードが発生する揚力を等しくするため、迎角を調整する装置が必要不可欠となる。
翼周りの現象と揚力発生原理
揚力とは翼体の上側より下側が高圧となる圧力差である。揚力の原理について、とくに、非圧縮とされる日常的な速度を対象としては、古今様々な説明が試みられてきたが決定的なものがない。突き詰めていくと「空気(連続体)がそういう性質だから」といった、物性に基づいた仮定が下敷きになっており、「飛行機が飛ぶ原理はわかっていない」と揶揄される現状がある。
- 非粘性/ポテンシャル流(非圧縮)
ポテンシャル流ではよどみ点の位置を予測できない。翼後ろ側のよどみ点が翼後端に固定されるという条件(クッタ条件)を課すことで揚力を計算できる。クッタ条件は粘性の効果のひとつと考えられる。
- 粘性流/境界層
粘性あり、すなわち境界層を考慮する場合には、翼と触れている流体要素は表面に付着し翼に対し停まっている(ノンスリップ)ため、表面速度から揚力を導くことはできない。境界層の外の速度場から計算する必要がある。これは翼型に境界層厚さを加味するということでもある。
- 非圧縮流れ
流速が音速よりはるかに低速の流れは非圧縮とみなされる。非圧縮場では、空気が翼体の通過によって押されるとき押された空気はつぶれることができず代わりに周辺の流路が狭まって流速が増す。流体要素の速度増減は圧力減増と対応し流速の高い部分は圧力は低い。これはベルヌーイ定理と呼ばれる。現実の流体要素でいうと、流路の狭まりに対し要素の流路への進行方向前側が先に進入するため要素が前後に引き伸ばされて圧力が下がる。
物体が空気中を移動すると物体前方で余剰となった空気は物体の上下を回り込んで物体背面側へと移動する。揚力ゼロの物体の場合は上下で回り込む量が同程度であるのに対し、揚力の大きい物体では上側でのみ回り込む(クッタ条件)。このとき物体の上側で流路が狭まり流速が増し、圧力が下がる。
揚力とは翼体の上側より下側が高圧となる圧力差である。これは非圧縮流の場合には速度変化を伴い、この積算量は循環と呼ばれる。揚力が生じているとき周囲の空気にはどこかで必ず逆向きの運動(ダウンウォッシュ)が起きる。ダウンウォッシュの周囲には渦が発生しうる。これらはいずれも揚力が生じているときの周囲の現象であり、揚力の発生機構ではない。発生機構としては、なぜ流体が翼面に沿って動くのか、後方よどみ点はなぜ物体の後縁にトラップされるのか(クッタ条件)といった点を省略せずに説明する必要がある。
- 超音速(圧縮性流れ)
超音速機のほうが揚力の一般向けの説明は容易である。(流体力学の知識が無いとき、空気が翼体に押されたときに空気がつぶれることを想像するため。)
薄板状の物体を迎角をつけて、空気中を音速を上回る速度で移動させる。物体下面(前面)では空気が翼により押しのけられるときにつぶれて高圧となる。背面側では逆に翼面に引っ張られた空気が希薄となり低圧となる。これにより迎角に依存した上向きの力が生じる。
実用上は前縁が鋭利であることが望ましい。実際の翼は菱がたの断面形状などが用いられる。
簡易的な説明として「飛び石説」と呼ばれる揚力解釈がある。
- 簡易的な説明
翼周りの流れや揚力の説明について、一般向けの簡易的な説明も様々に発案されている。以下に代表的なものをまとめる。
説明(説明の流れは左から右) 妥当性 カルマン渦との対比 単純な円筒や球の周りの流れでもカルマン渦が生じるような状況では瞬時的に揚力が生じてる。 これは物体前後のよどみ点や剥離の位置や物体上下左右の流速に余剰自由度と循環依存があり、初期値依存やヒステリシスが生じることの表れである。
野球ボールの縫い目のような突起があるとよどみ点や剥離点がトラップされ、時間平均したときの正味揚力も現れうる。 主流に対する偏向板(ダウンウォッシュの反作用) 主流に対して流れの方向を変える偏向板として説明する。 物体形状に沿うように局所の流動方向が変わり、翼の周囲や背後で下向き流れが発生。
全体として流れの方向が下へ偏向される。
流れを下向きに変えた反作用として翼は上に向かう。
「翼に沿った動き」という説明は密度変化を想起させるため非圧縮流れの説明として十分ではない。 非圧縮流れで「翼に沿った流れ」という説明は、特に翼の下面では実現象と合わない。
地上を滑る物体の揚力 車両のように地面のすぐ上を移動する半円形状の物体などを仮定して説明する。 上面が高速かつ低圧となることや循環を説明しやすい。
物体下面を考えなくてよいため単純である。 飛び石説 水面をはねる飛び石(水切り)に見立てた説明。 「翼体下面に空気がぶつかることで高圧領域が形成される」といった解釈。
圧縮性(超音速)流れの現象に近い。したがって日常の諸現象とは合致しない。 実際に空気が水面や噴流のように翼体下面に持続的にぶつかることはおきない。仮にぶつかった場合にも、流体は縮まず流路が狭まり圧力はむしろ下がる。
超音速機の翼の原理として説明するのであれば妥当。
循環説 翼周りの循環(回転成分、翼上下の速度差と似義)という量で説明がつく。クッタ・ジュコーフスキーの定理を重視する立場。 翼の上下流の合流が翼後縁からずれる状態は不安定だから現れないし考えなくてよい、すなわちクッタ条件を満たすことが前提の解説。
クッタ・ジュコーフスキーの定理はマグヌス効果の解析的な解であり[2]、揚力が流速の2乗と流体の密度に比例する式[3]。 なぜ翼の背面に沿うかという点については安定解だからといった程度の説明。
等時間通過説(同着説) 翼の前縁で上下に別れた気流は、等時間で通過して後縁で同着する。よって、翼の下面より上面の膨らみのほうが大きければ、より距離の長い上面の方が流速が速いので、上面の方が静圧が低くなる。 上向きの面の圧力積算量に対し下向き面の積算量が高値であるとき、上向きの揚力となる。 同着は観測手段が乏しかった時代の解釈で、誤り[4][5]。
上面と下面の流速の差により揚力が発生するというくだりは正しい[6]。流線曲率の定理に基づく説明 流線曲率の定理により、物体の上面と下面で流線が非対称に曲がっていると圧力差となる。 流線が得られている際の揚力説明の流儀のひとつである。
視覚的にわかり易いという点は優位。 アンダーソンの作用・反作用説[注釈 2] 翼上面の局所的に高速な空気は翼形に沿って流れる。このとき周囲の流体や壁面を引き込む。流体は下へ向かう。(噴流のコアンダ効果と同じという解釈) 翼背面の流れが後縁まで付着し続ける、クッタ条件の原因を説明している。
欠点が指摘された[7](どこ?)。 噴流以外にコアンダ効果を持ち出すべきでないという指摘[6]。
境界層が付着し続けることについてコアンダ効果を持ち込む必要なしという指摘。
原理に関する誤解説の例
 この節は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2019年5月)
この節は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2019年5月)飛行機の揚力については既に等角写像を用いた理論[詳細?]が構築されており厳密な計算が可能である一方、原理については完全に解明されたと言い切れない部分がある。「飛行機がなぜ飛ぶのか未だに分かっていない」といった言い方がされ、科学啓蒙書や航空工学の専門家の書物などでもこのような説明が書いてある。
本当は、飛行機がなぜ飛べるのかは分かっているのに、一般向けの文書には明らかに誤りを含んだ解説がある。
圧力と反作用の関係
揚力の解説の中には、反作用に言及が無いもの[8]や圧力分布に言及が無いといった簡易なものがある。
なかには反作用と圧力分布の一方を否定するものがあるが、圧力差こそが反作用であり、当に誤解である。下記の参考文献にもそのようにも解釈できるものが含まれる。
- 揚力は圧力差であり反作用はないという主張
- これは「翼を動かしたときに生じる圧力差」との区別しづらい状況でしばしば陥る誤解である。
- 翼面に垂直に働く駆動力は圧力場であり、これは流体から翼への作用である。このとき、作用反作用の法則の通り、流体側は正負逆の力を受ける。
- 揚力を議論しているときの流体の圧力差とは、主流中の翼体の運動によるものである。それが抗力と揚力の反作用でないなら、別の要因があり追加の説明が必要である。
- 揚力は圧力によるものではないという主張
- なら何の力によるかが示されていない。反作用は力の種類ではない。全ての力は基本相互作用が基になっているが、それまでの間か示されていない。「車両は路面からの反作用で走るが、車輪と路面との摩擦力は関係ない。」というようなものである。
- 翼の上下のように非対称でも圧力が同じというのは、流体動力学の基本のベルヌーイの定理に反する。
同着説(等時間通過説)
翼の上下の圧力差の発生原因において、下記のような説明がなされることがある。
- 翼は下面より上面の膨らみのほうが大きい。翼の前縁で上下に別れた気流は、後縁で同着する。よって、より距離の長い上面の方が流れが速く、ベルヌーイの定理によって気圧が下がり、揚力が発生する。
しかし、「翼の前縁で上下に別れた気流は、後縁で同着する。」という部分は誤りである。実際には同着しておらず[9]、下側の方が時間がかかり遅れる[7][6]。
そもそもこの発生原因では、背面飛行や上下対称の翼型の揚力の説明ができていない[7]。
「抗力と揚力の合力」

流れの中にある平板が受ける力は、現実には斜めの矢印で示した力であり、抗力と揚力は水平方向・垂直方向への分力に過ぎない。 抗力と揚力は、物体が流体から受ける正味の力の分力である。その元々の正味の流体力の呼称に困り「揚力と抗力の合力」といわれることがある。「…揚力と抗力が生じ、翼はその合力を受ける。」という表現も見られる。これは定義の循環である。前述の#揚抗比で説明した通り、揚力だけが独立して生じることは無い。
脚注
注釈
出典
- ^ “NACA 2412 (naca2412-il)”. airfoiltools.com. 2022年6月17日閲覧。
- ^ 法則の辞典. “クッタ‐ジューコフスキの定理”. コトバンク. 2020年5月20日閲覧。
- ^ 日本大百科全書(ニッポニカ). “クッタ‐ジュコフスキーの定理”. コトバンク. 2020年5月18日閲覧。
- ^ 「翼の原理」日本機械学会 流体工学部門
- ^ “Incorrect Lift Theory”. NASA(アメリカ航空宇宙局). 2019年5月4日閲覧。
- ^ a b c d 飛行機はなぜ飛ぶかのかまだ分からない?? - NPO法人 知的人材ネットワーク・あいんしゅたいん - 松田卓也による解説。
- ^ a b c 「新しい航空学 デビッド・アンダーソン氏の新理論」2011年11月19日
- ^ 「航空実用辞典」日本航空
- ^ Francis Villatoro (2008-02-17), how wings work? Smoke streamlines around an airfoil 2018年10月24日閲覧。
参考文献
 出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。
出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。- 日本機械学会編『流れのふしぎ』講談社ブルーバックス ISBN 978-4062574525 p168-169 p156-161
- 石綿良三『図解雑学 流体力学』ナツメ社 ISBN 978-4816343926 p218-219 p84-87
- 佐藤晃『よくわかる飛行機の基本と仕組み』秀和システム ISBN 978-4798028750 p55
- 水木新平・櫻井一郎 監修『飛行機のメカニズム』ナツメ社 ISBN 978-4-8163-4922-5 p8-34
関連項目
外部リンク
揚力
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/05/01 06:58 UTC 版)
翼に生じる空気力のうち、流れと垂直な成分。数式では L と表記されることが多い。
※この「揚力」の解説は、「翼」の解説の一部です。
「揚力」を含む「翼」の記事については、「翼」の概要を参照ください。
揚力
「揚力」の例文・使い方・用例・文例
揚力と同じ種類の言葉
- >> 「揚力」を含む用語の索引
- 揚力のページへのリンク


