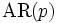自己回帰モデル

OR事典

自己回帰モデル

読み方：じこかいきもでる
【英】：autoregressive (AR) model

を の弱定常過程とし, を ,, のホワイトノイズとする. が と表現できるとき, このモデルを次数 の自己回帰モデルと呼び, モデルと略記する.AR という用語は を自身の過去の値に回帰することに由来し,AR モデルは理解しやすい構造をもっている.

ウィキペディア

自己回帰モデル

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/06/02 08:42 UTC 版)

自己回帰モデル（じこかいきモデル、英: autoregressive model）は時点 t におけるモデル出力が時点 t 以前のモデル出力に依存する確率過程である。ARモデルとも呼ばれる。

自己回帰モデルは、例えば自然科学や経済学において、時間について変動する過程を描写している。（古典的な）自己回帰モデルは実現値となる変数がその変数の過去の値と確率項（確率、つまりその値を完全には予測できない項）に線形に依存している。ゆえに自己回帰モデルは一種の確率差分方程式の形状を取る。

自己回帰モデルはより一般的な時系列の自己回帰移動平均モデル（ARMAモデル）の特別なケースである。また、一つ以上の確率差分方程式からなるベクトル自己回帰モデル（VARモデル）の特別ケースでもある。推計統計学・機械学習における生成モデルとしても自己回帰モデルは表現でき、古典的な（線形）自己回帰生成モデルを拡張した非線形自己回帰生成モデルも盛んに研究されている。

定義

$AR(p)$

AR(0); AR(1) with AR parameter 0.3; AR(1) with AR parameter 0.9; AR(2) with AR parameters 0.3 and 0.3; and AR(2) with AR parameters 0.9 and −0.8

最も単純なARモデルは AR(0) であり、項の間に依存関係がない。誤差/イノベーション/ノイズ項のみが過程の出力に寄与し、ゆえに図で示されているように AR(0) はホワイトノイズに対応する。

$\varphi$

ノイズ分散が $\mathrm {Var} (Z_{t})=\sigma _{Z}^{2}$ カテゴリ

ウィキペディア小見出し辞書

自己回帰モデル

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/11/18 11:22 UTC 版)

「自己回帰移動平均モデル」の記事における「自己回帰モデル」の解説

詳細は「自己回帰モデル」を参照 AR(p) という表記は次数 p の自己回帰モデルを表す。AR(p)モデルは次の式で表される。 X t = c + ∑ i = 1 p φ i X t − i + ε t . ここで φ 1 , … , φ p はモデルのパラメータ、 c は定数項、 ε t は誤差項（後述）である。定数項は単純化するために省かれることが多い。 自己回帰モデルは基本的に無限インパルス応答フィルタに一種の変形を加えたものである。 モデルとして定常的であるために、パラメータの値には何らかの制約が必要である。例えば、|φ1| > 1 となる AR(1)モデルは定常的ではない。