最小分散性

統計学用語辞典

最小分散性

　推定量の 有効性 を示す一つの指標として 最小分散性 が挙げられる。
　母平均値 μ，母分散 σ² の正規分布 N（μ，σ²）に従って分布する 2 つの独立な確率変数 X，Y から母平均 μ を推定する場合， a + b = 1　（ a ≧ 0， b ≧ 0 ）であれば，Z = a X + b Y は，E［ Z ］ = a E［ X ］ + b E［ Y ］ = ( a + b ) μ なので不偏推定量になる。しかし，a（または b）の選び方によって，確率変数 Z の作り方は無数にある。
　ところで，Z の分散は
　　V［Z］ = a² V［X］+ b² V［Y］ = ( a² + b² ) σ² ≧ 2 a b σ²
となるから，a = b = 1 / 2 つまり Z = ( X + Y ) / 2 のとき Z の分散は最小値 σ² / 2 をとる。
　このように，母数 θ の推定量 のなかで， の分散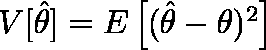
　　
を最小にする推定量は，最小分散推定量 と呼ばれ，推定量が満たすべき望ましい基準とされている。
　なお，不偏でしかも最小分散性を満たす推定量は，最良線形不偏推定量 と呼ばれる。