答え
例題は，二群の判別なので，答えを求める手順は若干簡単になる。
以下は実際の計算例であり，その説明は「マハラノビスの距離に基づく判別係数の求め方」の後半にある。
なお，二群の判別の場合には「相関比を最大にすることによる判別係数の求め方」によっても「同等の解」が求まる。「同等の解」というのは，全く同じ数値の解ではないが一方の解（係数と定数項の両方）が，もう一方の解の定数倍になっているということである。
- 各変数の平均値の差のベクトルは，
d= ( 3.5 - 7.5, 6.5 - 4.5 ) ' = ( - 4, 2 ) '
- 各群の変動・共変動行列は，
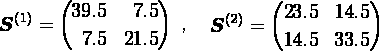
- プールした分散・共分散行列 Vは，各群の変動・共変動行列の和を「全データの個数−2」で割ったものである。
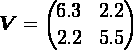
- よって，解くべき連立方程式は，
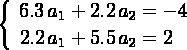
- これを解いて，a1 = - 0.88561，a2 = 0.71788 となるので，判別式 DF0 は，
DF0 = - 0.88561 X1 + 0.71788 X2 + c となる。
- c は任意に決めてよいが，各変数の「平均値の平均値」を判別式に代入して得られる数値の符号を変えたものにすると，DF の正負で群を判別できるので便利である。
今の場合は，平均値の平均値は，5.5，5.5 なので，DF0 = - 0.92251 となり，c = 0.92251 とする。
すなわち最終的な判別関数は，DF = - 0.88561 X1 + 0.71788 X2 + 0.92251。
- 判別結果は表 1，図 1 のようになる。
表 1．判別値および判別結果 群 ケース X1 X2 判別値 判別群 1 1 5 10 3.67326 1 1 2 0 7 5.94767 1 1 3 4 7 2.40523 1 1 4 8 6 -1.85508 2 1 5 2 5 2.74069 1 1 6 2 4 2.02281 1 2 1 10 8 -2.19054 2 2 2 7 7 -0.25159 2 2 3 9 5 -3.45857 2 2 4 5 3 -1.35190 2 2 5 9 2 -5.61221 2 2 6 5 2 -2.06978 2
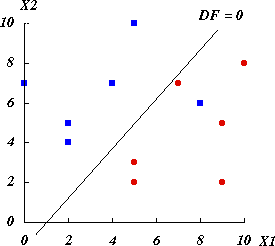
図 1．判別図
このページでは「統計学用語辞典」から答えを検索した結果を表示しています。
Weblioに収録されているすべての辞書から答えを検索する場合は、下記のリンクをクリックしてください。
全ての辞書から答え
を検索
Weblioに収録されているすべての辞書から答えを検索する場合は、下記のリンクをクリックしてください。
全ての辞書から答え
を検索
- >> 「答え」を含む用語の索引
- 答えのページへのリンク
