最適性条件 (非線形計画における)
【英】:optimality condition
概要
非線形計画問題において, 最適解が満たすべき条件, あるいは最適解になることを保証する条件の総称. 通常, それらは目的関数と制約関数の勾配ベクトルやヘッセ行列を用いて表現される. 最適性条件には, 1次の最適性条件, 2次の最適性必要条件, 2次の最適性十分条件等があるが, 最も基本的なのがカルーシュ・キューン・タッカー条件である.
詳説
非線形計画問題とは,有限個の不等式,等式制約条件の下で,目的関数を最小(最大)化する問題であり,次のように表される.
 | 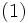 |
ここで  (
( は転置記号), 関数
は転置記号), 関数 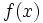 ,
,  ,
, は微分可能で,導関数は連続と仮定する.制約条件を満たす点
は微分可能で,導関数は連続と仮定する.制約条件を満たす点 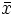 を実行可能解(以下,可能解という)と呼ぶ.任意の可能解
を実行可能解(以下,可能解という)と呼ぶ.任意の可能解 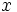 に対して
に対して  が成立するとき,
が成立するとき, 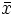 を最適解と呼ぶ.しかしながら,一般には非線形計画問題の最適解を求めることは容易ではなく,局所的に最適な解である局所的最適解を考えることが多い.即ち,可能解
を最適解と呼ぶ.しかしながら,一般には非線形計画問題の最適解を求めることは容易ではなく,局所的に最適な解である局所的最適解を考えることが多い.即ち,可能解 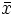 で,適当な半径
で,適当な半径  を選べば,
を選べば,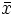 を中心とする半径
を中心とする半径  内にあるどの可能解
内にあるどの可能解 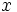 に対しても
に対しても  が成立するものを局所的最適解と呼ぶ.
が成立するものを局所的最適解と呼ぶ.
局所的最適解を求める際,局所的最適解が満たすべき条件,局所的最適解であることを保証する条件が基本的な役割を果たすが,それらを総称して最適性条件(optimality condition)と呼ぶ.通常,最適性条件は目的関数,制約関数の勾配ベクトル  や,
や,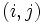 成分が
成分が  で定義されるヘッセ行列
で定義されるヘッセ行列  を用いて記述されるが,特に勾配ベクトルのみで表された最適性条件を1次の最適性条件(first-order optimality condition),ヘッセ行列も利用して表されたものを2次の最適性条件と呼ぶ.
を用いて記述されるが,特に勾配ベクトルのみで表された最適性条件を1次の最適性条件(first-order optimality condition),ヘッセ行列も利用して表されたものを2次の最適性条件と呼ぶ.
1次の最適性条件で,最もよく利用されるのが次の カルーシュ・キューン・タッカー条件(Karush-Kuhn-Tucker condition,KKT条件)である.
点 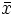 が局所的最適解ならば,後述する制約想定の下で,適当なベクトル
が局所的最適解ならば,後述する制約想定の下で,適当なベクトル  が存在して,ラグランジュ関数を
が存在して,ラグランジュ関数を  と定義するとき,次のKKT条件が成立する.
と定義するとき,次のKKT条件が成立する.
 |
ここで,ベクトル 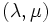 はラグランジュ乗数,条件
はラグランジュ乗数,条件  は相補性条件と呼ばれる.
は相補性条件と呼ばれる.
一方, KKT条件は次の等式,不等式系が解  を持たないことを,二者択一定理を用いて言い換えた条件でもある.
を持たないことを,二者択一定理を用いて言い換えた条件でもある.
 | 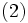 |
ただし, はアクティブな不等式制約, すなわち点
はアクティブな不等式制約, すなわち点 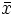 において等号が成り立つ不等式制約の集合を表わす.条件(2)に現れる集合
において等号が成り立つ不等式制約の集合を表わす.条件(2)に現れる集合  は実行可能集合
は実行可能集合  の,点
の,点 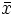 における近似集合と考えられるが,実際に良い近似になるのは,何らかの仮定を満たす場合に限られる.この種の仮定を総称して,制約想定 (constraint qualification,CQ),あるいは正則条件と呼ぶ.キューン・タッカーの制約想定をはじめとして,数多くの制約想定が提案されているが,なかでも1次独立制約想定(LICQ)とマンガサリアン・フロモヴィッツ条件(MF 条件)が重要である.
における近似集合と考えられるが,実際に良い近似になるのは,何らかの仮定を満たす場合に限られる.この種の仮定を総称して,制約想定 (constraint qualification,CQ),あるいは正則条件と呼ぶ.キューン・タッカーの制約想定をはじめとして,数多くの制約想定が提案されているが,なかでも1次独立制約想定(LICQ)とマンガサリアン・フロモヴィッツ条件(MF 条件)が重要である.
- LICQ:
 は1次独立である.
は1次独立である.
LICQ は MF 条件より強い仮定であり,LICQ が成立するとき,ラグランジュ乗数  は一意に決まる.他方,制約想定が満たされない場合でも,点
は一意に決まる.他方,制約想定が満たされない場合でも,点 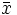 が局所的最適解ならば,ゼロでないベクトル
が局所的最適解ならば,ゼロでないベクトル  が存在して,次のフリッツ・ジョン条件が成立する.
が存在して,次のフリッツ・ジョン条件が成立する.
 |
フリッツ・ジョン条件は, のとき(従って
のとき(従って  としてよい),KKT 条件に一致する.これにより,
としてよい),KKT 条件に一致する.これにより, を保証する条件を制約想定と呼ぶことも多い.
を保証する条件を制約想定と呼ぶことも多い.
凸計画問題の場合, がKKT条件を満たせば,
がKKT条件を満たせば,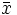 は最適解になる.しかし一般には,KKT条件は最適性を保証するとは限らない.最適性を詳しく調べるには,2次の最適性条件が必要になる.以下において,各関数は2回連続微分可能であると仮定する.即ち,2回までの偏導関数は全て連続とする.2次の最適性十分条件(second-order sufficient optimality condition)としては,次の定理がよく利用される.
は最適解になる.しかし一般には,KKT条件は最適性を保証するとは限らない.最適性を詳しく調べるには,2次の最適性条件が必要になる.以下において,各関数は2回連続微分可能であると仮定する.即ち,2回までの偏導関数は全て連続とする.2次の最適性十分条件(second-order sufficient optimality condition)としては,次の定理がよく利用される.
今, がKKT条件を満たすとする.さらに3つの条件 (a)
がKKT条件を満たすとする.さらに3つの条件 (a)  , (b)
, (b)  , (c)
, (c)  を満たすゼロベクトルでない任意の
を満たすゼロベクトルでない任意の  に対し,
に対し, が成立するならば,
が成立するならば,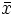 は孤立局所最適解になる.すなわち,適当な半径
は孤立局所最適解になる.すなわち,適当な半径  を選べば,
を選べば,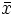 を中心とする半径
を中心とする半径  内にある任意の可能解
内にある任意の可能解  に対して,
に対して, が成立する.ここで,
が成立する.ここで, はラグランジュ関数の
はラグランジュ関数の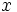 に関するヘッセ行列を表わす.
に関するヘッセ行列を表わす.
この十分条件と対をなす2次の最適性必要条件(second-order necessary optimality condition)としては,次の定理が知られている.
可能解 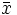 が局所的最適解で,
が局所的最適解で, はKKT条件を満たすとする.このとき,1次独立制約想定の下で,(a)-(c)を満たす任意の
はKKT条件を満たすとする.このとき,1次独立制約想定の下で,(a)-(c)を満たす任意の  に対し,
に対し, が成立する.
が成立する.
2次の最適性十分条件は,最適性の判定以外にも,安定性理論,感度分析,アルゴリズムの収束の議論において重要な役割を演じる.安定性理論(stability theory)と感度分析(sensitivity analysis)は,目的関数や制約関数を微小変化させたとき,最適解や最適値関数がどのように変化するかを調べる問題であり,主としてそれらの連続性を論じるのが安定性理論,微分可能性や変化率を取り扱うのが感度分析である.通常,パラメトリックな問題
 | 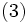 |
や,その一般化を舞台に,最適値関数  と最適解集合
と最適解集合  の挙動を考察する.ただし,
の挙動を考察する.ただし, はパラメータであり,
はパラメータであり, のとき(3)は非線形計画問題 (1) に一致するものとする.
のとき(3)は非線形計画問題 (1) に一致するものとする.
このとき, もし各関数が  に関して2回連続微分可能で,
に関して2回連続微分可能で,  が 3つの条件
が 3つの条件
すなわち, 全ての  に対し
に対し , を満たすならば,
, を満たすならば,  に十分近い任意の
に十分近い任意の 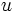 に対して, 問題 (3) に対するKKT条件を満たす
に対して, 問題 (3) に対するKKT条件を満たす  が
が  の近くにただひとつ存在する.また,それらは2回連続微分可能で,条件 (i)-(iii) を満たし,
の近くにただひとつ存在する.また,それらは2回連続微分可能で,条件 (i)-(iii) を満たし, は (3) の孤立局所最適解になる. さらに,それらの1回,2回の微分は (3) に対するKKT条件を用いて計算できる.この結果,ラグランジュ乗数が経済学の重要な概念であるシャドープライスを表すことがわかる.
は (3) の孤立局所最適解になる. さらに,それらの1回,2回の微分は (3) に対するKKT条件を用いて計算できる.この結果,ラグランジュ乗数が経済学の重要な概念であるシャドープライスを表すことがわかる.
[1] J.F. Bonnans and A. Shapiro, Perturbation Analysis of Optimization Problems, Springer, 2000.
[2] A.V. Fiacco, Introduction to Sensitivity and Stability Analysis in Nonlinear Programming, Academic Press, 1983.
[3] A.V. Fiacco and G.P. McCormick, Nonlinear Programming, SIAM, 1990.
- 最適性条件のページへのリンク
 は
は は
は を
を が
が