ぶんぷ‐かんすう〔‐クワンスウ〕【分布関数】
分布関数
2 個のサイコロを1000 回振って毎回の出た目の和を記録するという実験を行った結果を,表 1 の左半分に示す。
理論的に考察すると,目の和が最小であるのは,両方のサイコロが共に 1 の目が出たときであり,これは 1 / 36 の確率であることが分かる。目の和が 3 になるのは, ( 1, 2 ) という出方と ( 2, 1 ) という出方の 2 通りであり 2 / 36 となる。これをまとめると表 1 の右半分になる。
| 和xi | 度数 | 相対度数 | 累積相対度数 | 確率f(xi) | 分布関数F(xi) |
|---|---|---|---|---|---|
| 2 | 23 | 0.023 | 0.023 | 1/36=0.028 | 1/36=0.028 |
| 3 | 48 | 0.048 | 0.071 | 2/36=0.056 | 3/36=0.083 |
| 4 | 90 | 0.090 | 0.161 | 3/36=0.083 | 6/36=0.167 |
| 5 | 101 | 0.101 | 0.262 | 4/36=0.111 | 10/36=0.278 |
| 6 | 158 | 0.158 | 0.420 | 5/36=0.139 | 15/36=0.417 |
| 7 | 160 | 0.160 | 0.580 | 6/36=0.167 | 21/36=0.583 |
| 8 | 135 | 0.135 | 0.715 | 5/36=0.139 | 26/36=0.722 |
| 9 | 122 | 0.122 | 0.837 | 4/36=0.111 | 30/36=0.833 |
| 10 | 87 | 0.087 | 0.924 | 3/36=0.083 | 33/36=0.917 |
| 11 | 50 | 0.050 | 0.974 | 2/36=0.056 | 35/36=0.972 |
| 12 | 26 | 0.026 | 1.000 | 1/36=0.028 | 36/36=1.000 |
| 合計 | 1000 | 1.000 | 1.000 |
表 1 において,“相対度数”と“確率”の列,“累積相対度数”と“分布関数”の列の数値がかなり似ていることがわかる。
累積相対度数は 経験的分布関数 であり,その極限的なものが 理論的分布関数 F ( xi ) である(略して 分布関数 あるいは 確率分布 と呼ぶ。)。
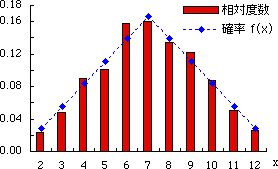 図 1.相対度数と確率 |
|---|
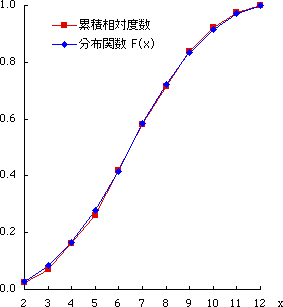 図 2.累積相対度数と分布関数 |
|---|
分布関数
分布関数
分布関数
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2017/08/26 13:03 UTC 版)
τ = 0でのグリーン関数G(τ)の不連続性のため、分布関数の評価は難しくなる。 次の和を評価するためにボソンとフェルミオンどちらの重み関数を選択することもできるが、結果は異なる。 G ( 0 ) = ∑ i ω ( i ω − ξ ) − 1 {\displaystyle G(0)=\sum _{i\omega }(i\omega -\xi )^{-1}} これは、G(τ)をτ = 0からわずかに遠ざけたとき、収束をコントロールするため、 G ( τ = 0 + ) {\displaystyle G(\tau =0^{+})} での重み関数として h η ( 1 ) ( z ) {\displaystyle h_{\eta }^{(1)}(z)} をとらなければならず、 G ( τ = 0 − ) {\displaystyle G(\tau =0^{-})} では h η ( 2 ) ( z ) {\displaystyle h_{\eta }^{(2)}(z)} をとらなければならないと理解できる。 ボソン G B ( τ = 0 − ) = 1 β ∑ i ω n e i ω n 0 + i ω n − ξ = − n B ( ξ ) , {\displaystyle G_{B}(\tau =0^{-})={\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {e^{i\omega _{n}0^{+}}}{i\omega _{n}-\xi }}=-n_{B}(\xi ),} G B ( τ = 0 + ) = 1 β ∑ i ω n e − i ω n 0 + i ω n − ξ = − ( n B ( ξ ) + 1 ) . {\displaystyle G_{B}(\tau =0^{+})={\frac {1}{\beta }}\sum _{i\omega _{n}}{\frac {e^{-i\omega _{n}0^{+}}}{i\omega _{n}-\xi }}=-(n_{B}(\xi )+1).} G F ( τ = 0 − ) = 1 β ∑ i ω m e i ω m 0 + i ω m − ξ = n F ( ξ ) , {\displaystyle G_{F}(\tau =0^{-})={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {e^{i\omega _{m}0^{+}}}{i\omega _{m}-\xi }}=n_{F}(\xi ),} G F ( τ = 0 + ) = 1 β ∑ i ω m e − i ω m 0 + i ω m − ξ = − ( 1 − n F ( ξ ) ) . {\displaystyle G_{F}(\tau =0^{+})={\frac {1}{\beta }}\sum _{i\omega _{m}}{\frac {e^{-i\omega _{m}0^{+}}}{i\omega _{m}-\xi }}=-(1-n_{F}(\xi )).}
※この「分布関数」の解説は、「松原振動数」の解説の一部です。
「分布関数」を含む「松原振動数」の記事については、「松原振動数」の概要を参照ください。
分布関数
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2017/08/26 13:03 UTC 版)
一般的表記 n η {\displaystyle n_{\eta }} はボース分布関数(η = +1)かフェルミ分布関数(η = −1)のどちらかを表す。 n η ( ξ ) = 1 e β ξ − η {\displaystyle n_{\eta }(\xi )={\frac {1}{e^{\beta \xi }-\eta }}} n η ( ξ ) = { n B ( ξ ) , if η = + 1 , n F ( ξ ) , if η = − 1. {\displaystyle n_{\eta }(\xi )={\begin{cases}n_{B}(\xi ),&{\text{if }}\eta =+1,\\n_{F}(\xi ),&{\text{if }}\eta =-1.\end{cases}}}
※この「分布関数」の解説は、「松原振動数」の解説の一部です。
「分布関数」を含む「松原振動数」の記事については、「松原振動数」の概要を参照ください。
- 分布関数のページへのリンク
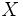
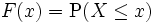 を
を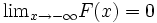 ,
, 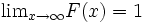 を
を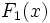 ,
, 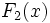
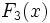 を
を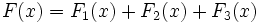 の形に
の形に