数量化IV類

統計学用語辞典

数量化 IV 類

　類似度行列を元にして，対象の二次元配置を求める。
　任意の基準による類似度行列を使用できるが，類似度行列は対称行列でなくてもよい。類似の方法として主座標分析がある。


　n 個の対象間の類似度を表す類似度行列を S = （ Sij ）とする。
　Sii = 0，対象 i と対象 j が似ていないほど負の，絶対値の大きな値をとるとする。類似度行列は対称行列でなくてもよい。
　数量化 IV 類は，各対象に数値を割当て，対象間のユークリッド距離が類似度の高い対象間では小さく，類似度の低い対象間では大きくなるようにすることを目的とする。
　まず，1 次元の数量化を考える。対象 i に ci，対象 j に cj という数値を割当てると，対象 i と対象 j の間のユークリッド平方距離は Δij² = （ ci - cj ）² となる。対象間のユークリッド距離が，類似度の高い対象間では小さく，類似度の低い対象間では大きくなるようにするので，( 1 ) 式で定義される Q が最大になるように ci，cj を定めればよいわけである。
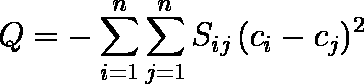　…… ( 1 )
　1 次元だけでは類似度を十分説明できない場合には，対象 i に（ ci1， ci2， ... ， cim ），対象 j に（ cj1， cj2， ... ， cjm ）のように数値を割り当てる。このとき，対象 i と対象 j の間の m 次元空間でのユークリッド平方距離 Δij² は（ 2 ）式のようになるので，これを（ 1 ）式に用いる。
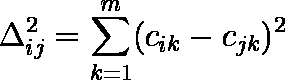　…… ( 2 )
（ 1 ）式は固有値問題を解くことになる。