チャップマン・コルモゴロフの等式
読み方：ちゃっぷまんこるもごろふのとうしき
【英】：Chapman-Kolmogorov equation
【英】：Chapman-Kolmogorov equation
マルコフ連鎖の推移確率が満たす等式. 状態空間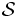
上の斉時的マルコフ連鎖の推移確率を
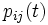とするとき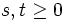, 任意の
と任意の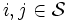
に対して
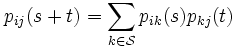
が成り立つ. これをチャップマン・コルモゴロフの等式と呼ぶ.
「OR事典」の他の用語
| 確率と確率過程： | コルモゴロフの後退方程式 サービス時間分布 シミュレーション チャップマン・コルモゴロフの等式 ファイナンシャルエンジニアリング ブラウン運動 ブロックガウス・ザイデル法 |
チャップマン-コルモゴロフの等式
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/07/14 01:31 UTC 版)
「マルコフ過程」の記事における「チャップマン-コルモゴロフの等式」の解説
チャップマン-コルモゴロフの等式は 3 つの時刻間の推移確率の間に成り立つ関係を示した等式で、時刻 s < t < u にたいして、 P ( s , u ; x , Z ) = ∫ P ( t , u ; y , Z ) P ( s , t ; x , d y ) {\displaystyle P(s,u;x,Z)=\int P(t,u;y,Z)P(s,t;x,dy)} で与えられる。すなわち、時刻 s に x を出発し時刻 u に Z に入る確率を、途中の時刻 t でどこにいたかで場合分けして計算したものである。
※この「チャップマン-コルモゴロフの等式」の解説は、「マルコフ過程」の解説の一部です。
「チャップマン-コルモゴロフの等式」を含む「マルコフ過程」の記事については、「マルコフ過程」の概要を参照ください。
ウィキペディア小見出し辞書の「チャップマン-コルモゴロフの等式」の項目はプログラムで機械的に意味や本文を生成しているため、不適切な項目が含まれていることもあります。ご了承くださいませ。
お問い合わせ。
- チャップマン-コルモゴロフの等式のページへのリンク
