スピアマンの順位相関係数
例題:
「表 1 において,変数 X と変数 Y の間のスピアマンの順位相関係数を求めなさい。」
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 変数 Xi | 2.8 | 3.4 | 3.6 | 5.8 | 7.0 | 9.5 | 10.2 | 12.3 | 13.2 | 13.4 |
| 変数 Yi | 0.6 | 3.0 | 0.4 | 1.5 | 15.0 | 13.4 | 7.6 | 19.8 | 18.3 | 18.9 |
計算手順:
- ケース数を n とする。
- 変数 X と変数 Y について,小さい方から順位をつける。同順位がある場合には平均順位をつける。
- 両者の順位の差をとり,di とする(Σ di = 0)。
- Σ di2 は 2 変数の順序の一致性の指標である。
このようなことから,次式を定義すれば, - 1 ≦ rs ≦ 1 となる。これがスピアマンの順位相関係数である。
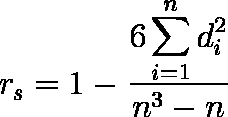
例題では,Σ di2 = 24 であるから,rs = 1 - 6・24 / ( 1000 - 10 ) = 0.85455 となる。
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 変数 Xi の順位 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 変数 Yi の順位 | 2 | 4 | 1 | 3 | 7 | 6 | 5 | 10 | 8 | 9 | |
| 順位の差 di | -1 | -2 | 2 | 1 | -2 | 0 | 2 | -2 | 1 | 1 | Σ di = 0 |
| 順位の差の二乗 di2 | 1 | 4 | 4 | 1 | 4 | 0 | 4 | 4 | 1 | 1 | Σ di2 = 24 |
注:
- どちらか一方(または両方)の変数において全てのケースが同一の値をとる
場合には,スピアマンの順位相関係数は定義できない。
- 同順位がある場合には,変数 X,変数 Y における同順位の個数を nx ,ny ,同順位の大きさを ti ,tj(i = 1,2, ... ,nx;j = 1,2, ... ,ny )としたとき,次式で計算される。同順位がない場合には Tx = Ty = 0 となり,前式に等しくなる。
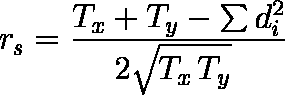
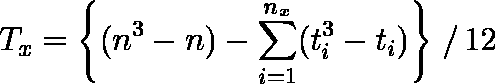
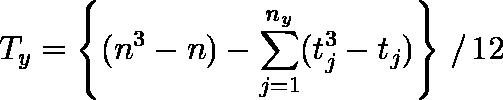
Weblioに収録されているすべての辞書からスピアマンの順位相関係数を検索する場合は、下記のリンクをクリックしてください。
 全ての辞書からスピアマンの順位相関係数
を検索
全ての辞書からスピアマンの順位相関係数
を検索
- スピアマンの順位相関係数のページへのリンク
