指数曲線

統計学用語辞典

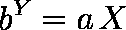指数曲線 - - 1

指数曲線 - - 1　　　　　Last modified: May 16, 2002
　　　　……(1)
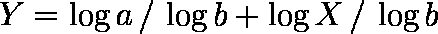　　　　……(2)

例題：
　「表 1 に示すようなデータに曲線をあてはめなさい。」

表 1．テストデータ

X	1	2	3	4	5	6	7	8	9	10
Y	0.631	1.262	1.631	1.893	2.096	2.262	2.402	2.524	2.631	2.727

考え方：

1. 元のデータをプロットすると図 1 のようになる。
   

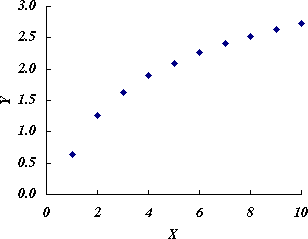
   図 1．元データのプロット

   
   
2. （ 1 ）式の表現において両辺の対数をとれば，（ 2 ）式の表現式になる。
   
3. c = log a / log b，d = 1 / log b，W = log X とおいて，Y = c + d W なる直線回帰を行えばよい。
   これは，図 1 の横軸を対数目盛りで描いたものが図 2 になる（データ点が直線上に並ぶ）ことを意味している。
   

   表 2．表 1 を変数変換したもの

   W=log(X)	0.000	0.693	1.099	1.386	1.609	1.792	1.946	2.079	2.197	2.303
   Y	0.631	1.262	1.631	1.893	2.096	2.262	2.402	2.524	2.631	2.727

   
   

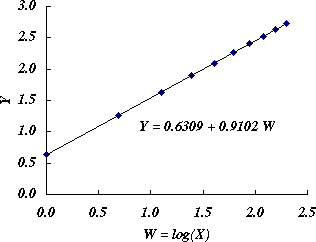
   図 2．変数変換後のプロット

   
   
4. 求めるパラメータは，b = exp ( 1 / d ) ，a = exp ( c / d ) となる。
   例題では，図 2 に示したように，c = 0.639，d = 0.9102 であるから，a = exp ( 0.6309 / 0.9102 ) = 2, b = exp ( 1 / 0.9102 ) = 3 となる（表 1 のデータは，この定数値に基づいて作成したものである）。

注：
b ＞ 1 のときは，図 1 のように，右上がりで上に凸の曲線になる。
1 ＞ b ＞ 0 のときは，図 3 のように，右下がりで下に凸の曲線になる。

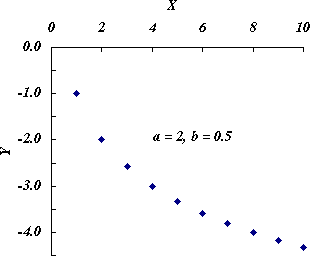図 3．1 ＞ b ＞ 0 のときの曲線の形

指数曲線 - - 2

指数曲線 - - 2　　　　　Last modified: Nov 07, 2002
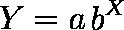　　　　……(1)

例題：
　「表 1 のに示すようなデータに曲線をあてはめなさい。」

表 1．テストデータ

X	1	2	3	4	5	6	7	8	9	10
Y	3.000	4.500	6.750	10.125	15.188	22.781	34.172	51.258	76.887	115.330

考え方：

1. 元のデータをプロットすると図 1 のようになる。
   

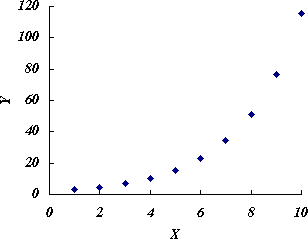
   図 1．元データのプロット

   
   
2. （ 1 ）式の両辺の対数をとり，log Y = log a + X log b とする。
   
3. c = log a，d = log b，V = log Y とおいて，V = c + d X なる直線回帰を行えばよい。
   これは，図 1 の縦軸を対数目盛りで描いたものが図 2 になる（データ点が直線上に並ぶ）ことを意味している。
   

   表 2．表 1 を変数変換したもの

   X	1	2	3	4	5	6	7	8	9	10
   V=log(Y)	1.099	1.504	1.910	2.315	2.720	3.126	3.531	3.937	4.342	4.748

   
   

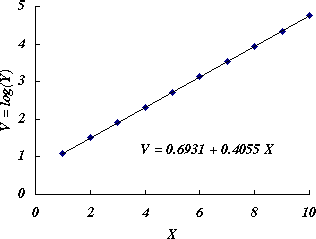
   図 2．変数変換後のプロット

   
   
4. 求めるパラメータは，a = exp c，b = exp d となる。
   例題では，図 2 に示したように，c = 0.6913，d = 0.4055 であるから，
   a = exp ( 0.6913 ) = 2, b = exp ( 0.4055 ) = 1.5 となる（表 1 のデータは，この定数値に基づいて作成したものである）。

注：
b ＞ 1 のときは，図 1 のように，右上がりで下に凸の曲線になる。
1 ＞ b ＞ 0 のときは，図 3 のように，右下がりで下に凸の曲線になる。

図 3．1 ＞ b ＞ 0 のときの曲線の形

指数曲線 - - 3

指数曲線 - - 3　　　　　Last modified: Nov 07, 2002
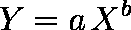　　　　……(1)

例題：
　「表 1 のに示すようなデータに曲線をあてはめなさい。」

表 1．テストデータ

X	1	2	3	4	5	6	7	8	9	10
Y	2	16	54	128	250	432	686	1024	1458	2000

考え方：

1. 元のデータをプロットすると図 1 のようになる。
   

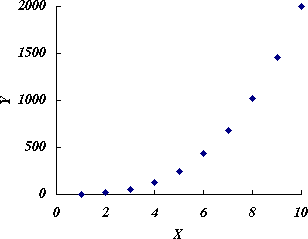
   図 1．元データのプロット

   
   
2. （ 1 ）式の両辺の対数をとり，log Y = log a + b log X とする。
   
3. c = log a，V = log Y，W = log X とおいて，V = c + b W なる直線回帰を行えばよい。
   これは，図 1 の縦軸と横軸を対数目盛りで描いたものが図 2 になる（データ点が直線上に並ぶ）ことを意味している。
   

   表 2．表 1 を変数変換したもの

   W=log(X)	0.000	0.693	1.099	1.386	1.609	1.792	1.946	2.079	2.197	2.303
   V=log(Y)	0.693	2.773	3.989	4.852	5.521	6.068	6.531	6.931	7.285	7.601

   
   

   図 2．変数変換後のプロット

   
   
4. 求めるパラメータは，a = exp c となる。
   例題では，図 2 に示したように，c = 0.6913，b = 3 であるから，
   a = exp ( 0.6913 ) = 2 となる（表 1 のデータは，この定数値に基づいて作成したものである）。

注：
b ＞ 1 のときは，図 1 のように，右上がりで下に凸の曲線になる。
1 ＞ b ＞ 0 のときは，図 3 のように，右上がりで上に凸の曲線になる。
b ＜ 0 のときは，図 4 のように，右下がりで下に凸の曲線になる。

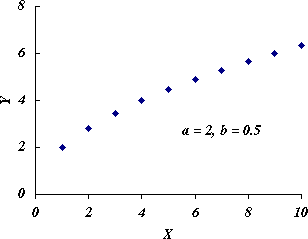図 3．1 ＞ b ＞ 0 のときの曲線の形	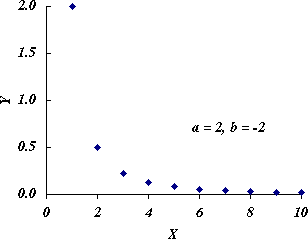図 4．b ＜ 0 のときの曲線の形