ホールの定理
読み方：ほーるのていり
【英】：Hall's theorem
【英】：Hall's theorem
2部グラフ 
において, 左側点集合 
に関する完全マッチングが存在するための必要十分条件は次のように書ける:
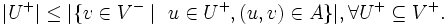
この不等式の右辺は,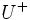 
中に左側点をもつ枝の右側点の数を表す.この必要十分条件をホールの定理と呼ぶ. ケーニグ・ホールの定理 (K\"onig--Hall's Theorem) と呼ばれることもある.
「OR事典」の他の用語
| グラフ･ネットワーク： | フェンシェル型双対定理 プリム法 ベルマン・フォード法 ホールの定理 ポリマトロイド マッチング マッチング問題 |
固有名詞の分類
このページでは「OR事典」からホールの定理を検索した結果を表示しています。
Weblioに収録されているすべての辞書からホールの定理を検索する場合は、下記のリンクをクリックしてください。
全ての辞書からホールの定理
を検索
Weblioに収録されているすべての辞書からホールの定理を検索する場合は、下記のリンクをクリックしてください。
全ての辞書からホールの定理
を検索
- ホールの定理のページへのリンク
