主成分とは何か
主成分分析の目的は,なるべく少ない合成変数で,なるべく多くの情報を把握するという 情報の縮約 である。
標準化された 2 変数 x1,x2 を考えたとき,図 1 のように座標軸 x1,x2 で表されるものを,座標軸 f1,f2 で表すことを考える。
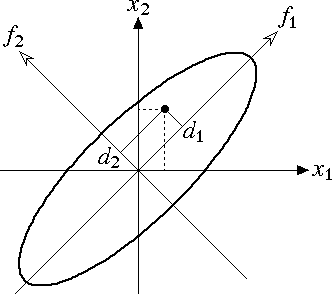 図 1.主成分分析とは何か |
|---|
これは座標軸の回転であり,回転角 θ = 45 度としたとき,
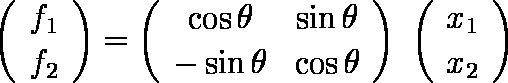
すなわち,
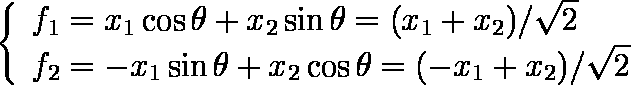
である。
f1 は最も分散( 情報量 )の大きい軸,f2 は f1 と直交して,次に分散の大きい軸である。f1 は x1,x2 と最も相関が高い。
f2 は f1 とは全く別の基準である。つまり,f1 と f2 が直交するということは,f1 と f2 は無相関であることを意味する。
もし,f1 の分散が f2 の分散に比べて大きければ,f1 だけで評価することができる。すなわち,元の 2 変数を“同時に”考慮する代わりに,1 個の合成変数“だけ”を考えればよいことになる。
変数が 3 個以上の場合も同様に考えることができる。元の変数が p 個ある場合も,m < p であるような少数個の合成変数を考えればよい。
ここで重要なのは,考慮すべき変数の個数が少なくなることだけではなく,各合成変数間の相関が 0 であることから,“個々の合成変数を独立に評価してよい”ということである(逆にいえば,変数間に相関がある限り,各変数を個別に評価することは“できない”ということである)。
- 主成分とは何かのページへのリンク
