主成分の求め方

統計学用語辞典

主成分の求め方

1. p 個の変数を X1， X2， ... ， Xp，これらの重み付け合成変量を Z1， Z2， ... ， Zm とする ( m ≦ p ) 。
   
   
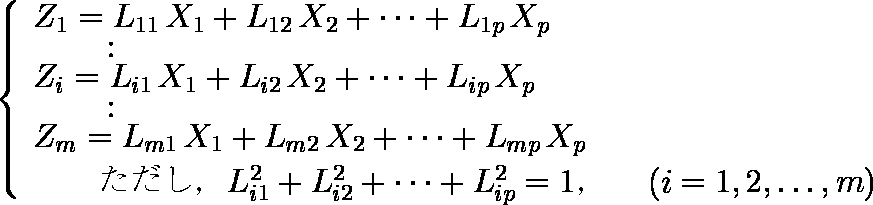
2. このような m 個の合成変量において，以下のような性質を持つものを考える。
   
   • 各合成変量の相関が 0 である。
   • 合成変量の分散 Var ( Zi ) は，Var ( Z1 ) ≧ Var ( Z2 ) ≧ … ≧ Var ( Zm ) である。
   
   
3. p 個の変数の相関係数行列の固有値を λ1 ≧ λ2 ≧ … ≧ λi ≧ … ≧ λm ≧ … ≧ λp ≧ 0 としたとき，λi に対応する固有ベクトルを重みとした合成変量が Zi に対応し，Zi の分散が λi に等しくなる（ 固有ベクトルは互に直交する，すなわち，互に相関が 0 である ）。
   
4. Z1， Z2， ... ， Zm は主成分と呼ばれ，そのうちで最も分散の大きい Z1 は第 1 主成分，次に分散の大きい Z2 は第 2 主成分，以下順に第 m 主成分と呼ばれる。
   
5. 各主成分と，もとの各変数の間の相関係数は因子負荷量と呼ばれる。因子負荷量は，第 i 主成分の重み Li1， Li2， ... ， Lip に，対応する固有値の平方根をかけたものである。すなわち，Zi と変数 X1 の相関係数は a1i = Li1 √(λi)，Zi と変数 X2 の相関係数は a2i = Li2 √(λi) などとなる。
   
6. 主成分分析の結果を表 1 のように表す。
   

   表 1．主成分分析の結果の表現

   	第1主成分	第2主成分	…	第m主成分	寄与率
   X1	a11	a12	…	a1m	Σa1k2
   X2	a21	a22	…	a2m	Σa2k2
   ：	：	：	…	：	：
   Xp	ap1	ap2	…	apm	Σapk2
   固有値	Σaj12	Σaj22	…	Σajm2
   寄与率	Σaj12/p	Σaj22/p	…	Σajm2/p

   
   
7. 寄与率 の欄は，各変数が m 個の主成分でどれくらい説明されるかを表す（ 0 ≦ 寄与率 ≦ 1 ）。
   
8. もう一つの寄与率は，各主成分がもとの情報をどれくらい説明しているかを表すもので，相関係数から出発した主成分分析の場合には，p 個の変数の持つ情報量の合計は p であるので，例えば第 1 主成分の寄与率は 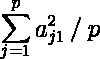である。