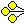
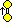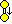ディンキン図形
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/04/17 01:16 UTC 版)
有限ディンキン図形
| 階数 | 古典型リー群 | 例外型リー群 | ||||
|---|---|---|---|---|---|---|
| A1+ | B2+ | C2+ | D2+ | E3–8 | G2 / F4 | |
| 1 | A1 
|
|||||
| 2 | A2   
|
B2  
|
C2 = B2  
|
D2 = A1xA1
|
G2  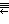 
| |
| 3 | A3    
|
B3    
|
C3    
|
D3 = A3 
|
E3 = A2xA1    
|
|
| 4 | A4      
|
B4      
|
C4      
|
D4   
|
E4 = A4    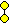
|
F4      
|
| 5 | A5        
|
B5        
|
C5        
|
D5     
|
E5 = D5    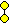  
|
|
| 6 | A6           
|
B6           
|
C6           
|
D6        
|
E6     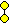    
| |
| 7 | A7             
|
B7             
|
C7             
|
D7          
|
E7     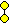      
| |
| 8 | A8               
|
B8               
|
C8               
|
D8            
|
E8     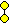        
| |
| 9 | A9                 
|
B9                 
|
C9                 
|
D9              
|
||
| 10+ | .. | .. | .. | .. | ||
アファインディンキン図形
ディンキン図形の拡張、すなわちアファインディンキン図形が存在する;これらはアファインリー環のカルタン行列を分類する。これらは (Kac 1994, Chapter 4, pp. 47–) において分類され、特に (Kac 1994, pp. 53–55) にリストされている。アファイン図形は X(1)
l , X(2)
l , X(3)
l と書かれる、ただし X は対応する有限図形の文字で、指数はアファイン図形のどの列にそれらが入っているかに依存する。これらの第一、X(1)
l は、もっとも一般的で、拡大ディンキン図形 (extended Dynkin diagram) と呼ばれ、チルダで表され、時には右上に + の記号をつけることもある[14]、例えば 
拡大ディンキン図形の集合、追加の頂点は緑(Bn に対しては n ≥ 3, Dn に対しては n ≥ 4)
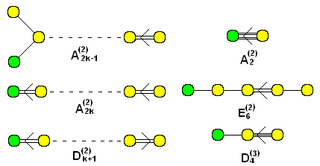
"Twisted" アファイン形は (2) あるいは (3) の上付き添え字で名づけられる。
(k はグラフの黄色の頂点の個数)
以下が頂点の個数が10個までのアファイン群に対するディンキングラフのすべてである。拡大ディンキングラフは、上の有限グラフに1つの頂点を加えた ~ 族として与えられる。他の有向グラフの変種は、位数の高い群の folding を表す値が (2) か (3) の上付き添え字とともに与えられる。これらは 「twistedアファイン」図形とカテゴライズされる[15]。
| 階数 |   
|   
|
|||
|---|---|---|---|---|---|
| 3 | 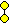 
|
              
|
 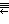     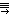   
| ||
| 4 |   
|
  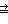    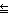 
|
                    
|
||
| 5 | 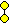   
|
    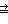      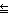 
|
                          
|
  
|
                 
|
| 6 |     
|
      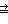        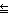 
|
                                
|
    
|
|
| 7 | 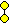     
|
        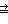          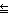 
|
                                      
|
      
|
       
|
| 8 |       
|
          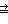            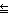 
|
                                            
|
        
|
       
|
| 9 | 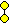       
|
            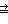              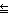 
|
                                                  
|
          
|
    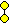          
|
| 10 |         
|
              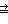                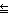 
|
                                                        
|
            
|
|
| 11 | ... | ... | ... | ... |
双曲型および高次のディンキン図形
コンパクトおよび非コンパクトな双曲ディンキングラフはすべて列挙されている[16]。階数 3 の双曲グラフはすべてコンパクトである。コンパクト双曲ディンキン図形は階数 5 まで存在し、非コンパクト双曲グラフは階数 10 まで存在する。
| 階数 | コンパクト | 非コンパクト | 計 |
|---|---|---|---|
| 3 | 31 | 93 | 123 |
| 4 | 3 | 50 | 53 |
| 5 | 1 | 21 | 22 |
| 6 | 0 | 22 | 22 |
| 7 | 0 | 4 | 4 |
| 8 | 0 | 5 | 5 |
| 9 | 0 | 5 | 5 |
| 10 | 0 | 4 | 4 |
コンパクト双曲ディンキン図形
| 階数 3 | 階数 4 | 階数 5 | |
|---|---|---|---|
| 線型グラフ | 巡回グラフ | ||
非コンパクト (Over-extended forms)
M理論のように理論物理学において用いられるいくつかの表記は拡大群に対し "~" の代わりに "+" の上付き添え字を用い、これにより higher extensions groups が定義できる。
- Extended ディンキン図形(アファイン)は "+" で与えられ1つの付け加えられた頂点を表す("~" と同じ)。
- Over-extended ディンキン図形(双曲)は "^" あるいは "++" で与えられ、2つの付け加えられた頂点を表す。
- Very-extended ディンキン図形で3つの頂点が付け加えられたものは "+++" で与えられる。
238個の双曲群(コンパクト・非コンパクト)
階数 n ≥ 3 の238個の(コンパクトおよび非コンパクト)双曲群は H(n)
i と名付けられ、各階数に対して i = 1, 2, 3, ... とリストされている。

|

|

|

| |||

|

|

|

| |||

|

|

|

|
Very-extended
Very-extended 群はローレンツ群であり、有限群に3つの頂点を加えることで定義される。E8, E7, E6, F4, G2 は very-extended 群で終わる6つの列を提供する。示されていない他の extended series は各 n に対して異なる列として An, Bn, Cn, Dn から定義できる。付随するカルタン行列の行列式は列がどこで有限(正)からアファイン(零)から非コンパクト双曲群(負)に変わるかを決定し、1つの時間的次元を用いて定義できるローレンツ群として終わり、M理論において用いられる[17]。
| 有限 | A2 | C2 | G2 |
|---|---|---|---|
| 2 | A2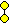
|
C2 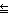 
|
G2 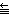 
|
| 3 | A2+= 
|
C2+= 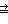  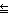 
|
G2+= 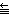   
|
| 4 | A2++   
|
C2++ 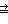  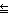   
|
G2++ 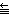     
|
| 5 | A2+++     
|
C2+++ 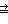  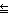     
|
G2+++ 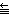       
|
| Det(Mn) | 3(3 − n) | 2(3 − n) | 3 − n |
注
出典
- ^ Baez, John (April 13, 1998), This Week's Finds in Mathematical Physics (Week 119)
- ^ Fulton & Harris 1991, Proposition D.40.
- ^ a b c Outer automorphisms of simple Lie Algebras
- ^ & Humphreys 1972, Section 16.5.
- ^ Jacobson 1971, section 7.
- ^ Algebraic geometry and number theory: in honor of Vladimir Drinfeld's 50th Birthday, edited by Victor Ginzburg, p. 47, section 3.6: Cluster folding
- ^ a b Folding by Automorphisms, John Stembridge, 4pp., 79K, 20 August 2008, Other Articles by John Stembridge
- ^ これらの foldings の絵と文献については次を参照:(Stekolshchik 2008, p. 102, remark 5.4).
- ^ Zuber, Jean-Bernard. Generalized Dynkin diagrams and root systems and their folding. pp. 28–30.
- ^ a b Transformations of Dynkin Diagrams, John Armstrong, March 5, 2010
- ^ a b (Knapp 2002, p. 758)
- ^ a b c Why are the Dynkin diagrams E6, E7 and E8 always drawn the way they are drawn?
- ^ Notes on Coxeter Transformations and the McKay correspondence, Rafael Stekolshchik, 2005, Section 2.1 The Cartan matrix and its Tits form p. 27. [1]
- ^ 例えば次を参照: Reflection groups and Coxeter groups, by James E. Humphreys, p. 96
- ^ [2] Infinite dimensional Lie algebras, Victor Kac
- ^ Carbone, L, Chung, S, Cobbs, C, McRae, R, Nandi, D, Naqvi, Y, and Penta, D: Classification of hyperbolic Dynkin diagrams, root lengths and Weyl group orbits, J. Phys. A: Math. Theor. 43 155209, 2010, arXiv:1003.0564
- ^ The symmetry of M-theories, Francois Englert, Laurent Houart, Anne Taormina and Peter West, 2003
- ディンキン図形のページへのリンク