集合の分割 分割の細分

ウィキペディア

集合の分割

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/08/19 14:18 UTC 版)

分割の細分

集合 X の分割 π が集合 X の分割 ρ の細分 (refinement) であるとは、π の個々の元が全て ρ のいずれかの元の部分集合であることを言う。大雑把に言えば、π の方が p よりも分割が細かい。これを π ≤ ρ と表記することもある。

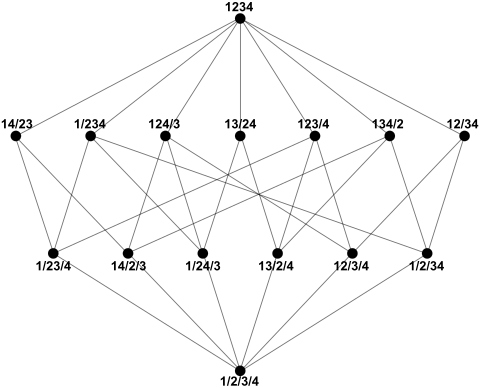
X の分割の集合におけるこの「より細かい」関係は半順序であり（そのため "≤" で表すのが適当）、実のところ完備束である。例えば、X = {1, 2, 3, 4} の「分割束」には15の元があり、以下のハッセ図で表される。

もう1つの例として、同値関係の観点から分割を細分化する方法を述べる。D を一般的なトランプの52枚のカードの集合とする。D における「色が同じ」という関係を ~_C などと表記する。このとき2つの同値類、{赤いカード} という集合と {黒いカード} という集合が得られる。この ~_C に対応した2ブロックの分割には「スートが同じ」という関係 ~_S による細分が存在し、4つの同値類 {スペード}、{ダイヤ}、{ハート}、{クラブ} が得られる。

非交差な分割

自然数の集合 N = {1, 2, ..., n} の同値関係 ~ に対応した分割が非交差 (noncrossing) であるとは、N 内のそれぞれ別の数 a、b、c、d が a < b < c < d という大小関係で、しかも a ~ c および b ~ d ということがない場合である。 上記のX = {1, 2, 3, 4} では、13/24のみが非交差ではない分割である． 有限集合の非交差な分割の束は、自由確率論において重要であることが近年わかってきた。2つの束の結びをとる操作が合致しないため、これらは全ての分割の束の部分集合を形成するが、部分束ではない。

各種分割の数え上げ

n 個の元を持つ集合の分割の総数はベル数 B_n である。n の小さいベル数を列挙すると、B₀ = 1、B₁ = 1、B₂ = 2、B₃ = 5、B₄ = 15、B₅ = 52、B₆ = 203 となっている。ベル数は次の漸化式で表される。

$B_{n+1}=\sum _{k=0}^{n}{n \choose k}B_{k}$

そして、次のような指数型母関数が存在する。

$\sum _{n=0}^{\infty }{\frac {B_{n}}{n!}}z^{n}=e^{e^{z}-1}$

n 個の元を持つ集合を k 個のブロックに分ける分割の総数は、第2種スターリング数 S(n, k) である。

n 個の元を持つ集合の非交差な分割の総数はカタラン数 C_n であり、次の式で表される。

$C_{n}={1 \over n+1}{2n \choose n}$