四色定理 証明のアイディアの概要

ウィキペディア

四色定理

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/03/23 13:51 UTC 版)

証明のアイディアの概要

以下の議論はEvery Planar Map is Four Colorable (Appel & Haken 1989)の序論に基づく要約である。欠点はあるが、ケンペの4色定理の最初の証明とされるものは、後に4色定理の証明に使われる基本的なツールの一部を提供した。ここでの説明は、上記の現代グラフ理論の定式化の観点から言い直したものである。

ケンペの議論は次のようなものである。まず，グラフで区切られた平面領域が三角分割されていない場合，つまり，境界にちょうど3つの辺がない場合，境界のない外側の領域も含めてすべての領域を三角形にするために，新しい頂点を導入することなく辺を追加することができる．この三角化グラフが4色以下で着色可能であれば，辺を削除しても同じ着色法が成り立つので，元のグラフも同様である．したがって，三角形化されたグラフの4色定理を証明するには，すべての平面グラフについて証明すれば十分であり，一般性を損なうことなくグラフが三角形化されていると仮定する．

頂点、辺、領域（面）の数を v, e, f とする。各領域は三角形であり、各辺は2つの領域で共有されるので、2e=3fとなる。これはオイラーの多面体定理v- e + f = 2 を使えば、6v- 2e = 12.さて、頂点の次数とは、その頂点に接する辺の数である。v_nを次数nの頂点の数、Dを任意の頂点の最大次数とする、

$6v-2e=6\sum _{i=1}^{D}v_{i}-\sum _{i=1}^{D}iv_{i}=\sum _{i=1}^{D}(6-i)v_{i}=12.$

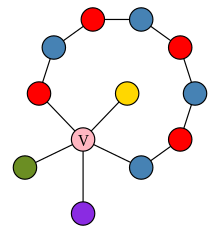
A graph containing a Kempe chain consisting of alternating blue and red vertices

先ほどと同様に、頂点vを取り除き、残った頂点を4色に着色する。もしvの4つの隣がすべて異なる色、例えば時計回りの順序で赤、緑、青、黄であれば、赤と青の隣を結ぶ赤と青の頂点の交互のパスを探す。このような経路はケンプ鎖と呼ばれる。赤と青の隣同士を結ぶケンペ鎖があるかもしれないし，緑と黄の隣同士を結ぶケンペ鎖があるかもしれない．連鎖していないのは赤と青の隣同士だとする。赤と青の交互のパスで赤の隣の頂点に接続されているすべての頂点を探索し、これらのすべての頂点で赤と青の色を逆にする。その結果、やはり4色使いになり、vを戻して赤に着色することができる。

これで残るのは次数5の頂点がGにある場合だけであるが、ケンペの議論にはこの場合の欠陥があった。HeawoodはKempeの間違いに気付くと同時に、5色しか必要でないことを証明することで満足するのであれば、（最小反例が6色を必要とすることだけを変えて）上記の議論を実行し、次数5の状況でKempeの鎖を使って五色定理を証明することができることに気付いた。

いずれにせよ、この次数5の頂点のケースを扱うには、頂点を取り除くよりも複雑な概念を必要とする。むしろ、（Gの）各頂点の次数が指定されたGの連結部分グラフである構成を考えることに議論の形式が一般化される。例えば、次数4の頂点の状況で説明されるケースは、Gにおいて次数4であるとラベル付けされた1つの頂点からなる構成である。上記と同様に、構成を削除して残りのグラフを4色化した場合、構成を再び追加したときに4色化も拡張できるように色付けを修正できることを示せば十分である。これが可能な構成を還元可能な構成と呼ぶ．ある構成の集合のうち少なくとも1つがGのどこかに必ず出現する場合、その集合を不可避な構成と呼ぶ。上の議論は、まず5つの構成（次数1の頂点、次数2の頂点、...、次数5の頂点）からなる不可避的な集合を与え、最初の4つが還元可能であることを示した。

Gは三角形であり、構成中の各頂点の次数は既知であり、構成内部の辺はすべて既知であるため、与えられた構成に隣接するGの頂点の数は決まっており、それらはサイクルで結ばれる。これらの頂点は配置の環を形成する。環にk個の頂点を持つ配置はk環構成であり、環を持つ配置は環構成と呼ばれる。上記の単純な場合と同様に、リングのすべての異なる4つのカラーリングを列挙することができる。構成のカラーリングに変更することなく拡張できるカラーリングは、最初は良いと呼ばれる。例えば、3つ以下の近傍を持つ上記の単一頂点の配置は、最初は良い配置であった。一般に、リングのカラーリングを良いものに変えるためには、上の4つの近傍がある場合のように、周囲のグラフを系統的に再カラーリングする必要がある。リングの4つのカラーリングの数が多いので、これはコンピュータの支援を必要とする主要なステップである。

最後に、この手順で漸化できる構成の不可避集合を特定することが残る。このような集合を発見するために使われる主要な方法は、放電法である。放電法の根底にある直感的な考え方は、平面グラフを電気的なネットワークとして考えることである。最初に正負の「電荷」が頂点に分配され、合計が正になるようにする。

上の式を思い出してほしい：

$\sum _{i=1}^{D}(6-i)v_{i}=12.$