制約なし最適化
【英】:unconstrained optimization
概要
実数値関数 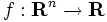 が与えられたとき,
が与えられたとき, 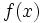 を変数
を変数 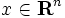 について最小化もしくは最大化する問題を制約なし最適化問題という. このとき
について最小化もしくは最大化する問題を制約なし最適化問題という. このとき 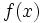 は目的関数と呼ばれる.
は目的関数と呼ばれる.
詳説
関数 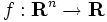 が与えられたときに,
が与えられたときに,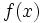 を変数
を変数 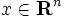 について最小化(もしくは最大化)する問題を制約なし最適化 (unconstrained optimization) 問題という.ここで,
について最小化(もしくは最大化)する問題を制約なし最適化 (unconstrained optimization) 問題という.ここで,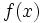 を目的関数という.ある
を目的関数という.ある 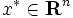 に対して
に対して
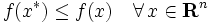 |
が成り立つとき,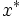 を最適解,あるいは大域的最適解という.また,ある
を最適解,あるいは大域的最適解という.また,ある 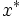 とその適当な近傍
とその適当な近傍 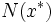 に対して
に対して
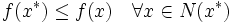 |
が成り立つとき,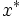 を局所的最適解という.
を局所的最適解という.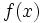 が
が 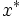 で微分可能であるとき,
で微分可能であるとき,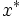 が局所的最適解ならば
が局所的最適解ならば
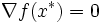 |
が成り立ち,さらに2回微分可能ならば,ヘッセ行列 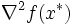 は半正定値行列になる.逆に,
は半正定値行列になる.逆に,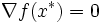 が成り立ち,かつ,
が成り立ち,かつ,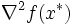 が正定値行列ならば,
が正定値行列ならば,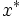 は局所的最適解になる.こうした最適性条件に基づいて,多くの数値解法は停留点,すなわち
は局所的最適解になる.こうした最適性条件に基づいて,多くの数値解法は停留点,すなわち 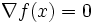 を満たす点
を満たす点 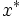 を見つけることを目指している.
を見つけることを目指している.
制約なし最適化問題を解くための数値解法は,目的関数値の情報だけを用いる直接探索法と微分の情報を用いる勾配法 (gradient method) とに大別される[2, 3, 4, 5].勾配法は反復法に分類されるもので,適当な初期点 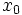 から出発して,
から出発して,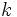 回目の反復で近似解
回目の反復で近似解 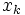 と探索方向
と探索方向 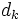 が与えられたときに
が与えられたときに
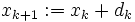 |
によって点列 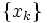 を生成していくものである.このとき探索方向の決め方によっていろいろな数値解法が考えられる.探索方向を決めるために,目的関数を何らかの意味で近似したモデル関数を局所的に最小化することが考えられている.モデル関数として,1次モデルと2次モデル
を生成していくものである.このとき探索方向の決め方によっていろいろな数値解法が考えられる.探索方向を決めるために,目的関数を何らかの意味で近似したモデル関数を局所的に最小化することが考えられている.モデル関数として,1次モデルと2次モデル
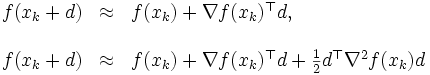 |
がよく用いられる.1次モデル最小化に基づいた解法として最急降下法 (steepest descent method) がある.この方法は探索方向を 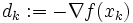 に選ぶものである.他方,2次モデル最小化に基づいた解法には,ニュートン法 (Newton's method),準ニュートン法 (quasi-Newton method),共役勾配法 (conjugate gradient method)などがある.ニュートン法は連立1次方程式
に選ぶものである.他方,2次モデル最小化に基づいた解法には,ニュートン法 (Newton's method),準ニュートン法 (quasi-Newton method),共役勾配法 (conjugate gradient method)などがある.ニュートン法は連立1次方程式
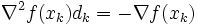 |
を解いて探索方向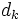 を決定する.また,準ニュートン法はヘッセ行列を行列
を決定する.また,準ニュートン法はヘッセ行列を行列 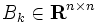 で近似して,連立1次方程式
で近似して,連立1次方程式
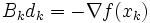 |
を解いて探索方向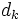 を決定する.その際,勾配ベクトル
を決定する.その際,勾配ベクトル 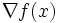 の情報を含んだ更新公式を利用して
の情報を含んだ更新公式を利用して 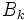 を逐次生成していくのが特徴である.いろいろな更新公式が提案されているが,特にBroyden-Fletcher-Goldfarb-Shanno (BFGS) 公式が有効であることが認められている.共役勾配法はこれらとは異なった立場の解法で,探索方向は
を逐次生成していくのが特徴である.いろいろな更新公式が提案されているが,特にBroyden-Fletcher-Goldfarb-Shanno (BFGS) 公式が有効であることが認められている.共役勾配法はこれらとは異なった立場の解法で,探索方向は
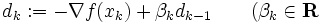 は適当なパラメータ は適当なパラメータ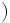 |
で定義される.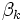 の選び方として Fletcher-Reeves公式やPolak-Ribiére-Polyak公式がある.ここで,ニュートン法が2階偏導関数を用いているのに対して,準ニュートン法や共役勾配法は1階偏導関数しか利用しないことに注意されたい.
の選び方として Fletcher-Reeves公式やPolak-Ribiére-Polyak公式がある.ここで,ニュートン法が2階偏導関数を用いているのに対して,準ニュートン法や共役勾配法は1階偏導関数しか利用しないことに注意されたい.
数値解法の有効性を特徴づける指標として局所的な収束の速さの尺度である収束率 (rate of convergence) と初期点の選び方によらず停留点への収束を保証する大域的収束性 (global convergence) がある.収束率の観点からみれば,最急降下法は高々1次収束しかしない方法,ニュートン法は2次収束する方法,BFGS公式を用いた準ニュートン法は超1次収束する方法であるといえる.実用的には,超1次収束や2次収束する方法であることが望ましい.他方,大域的収束性はそのままでは達成出来ないので,何らかの補助手段を必要とする.代表的な手段として直線探索法 (line search method) と信頼領域法 (trust region method) がある.直線探索法は,探索方向 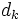 が与えられたときに,その方向でステップ幅
が与えられたときに,その方向でステップ幅 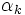 を調節して関数の減少
を調節して関数の減少 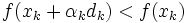 を実現し,
を実現し,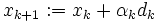 とおく.直線探索の枠組みで,最急降下法,準ニュートン法,共役勾配法の大域的収束性が示されている.それに対して信頼領域法は,2次モデルによる近似が妥当であると思われる領域で2次モデルを最小化するステップ
とおく.直線探索の枠組みで,最急降下法,準ニュートン法,共役勾配法の大域的収束性が示されている.それに対して信頼領域法は,2次モデルによる近似が妥当であると思われる領域で2次モデルを最小化するステップ 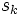 を選んで
を選んで 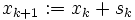 とする解法である.2次モデルでヘッセ行列を用いた場合(ニュートン法に対応する)やその近似行列を用いた場合(準ニュートン法に対応する)の信頼領域法の大域的収束性が示されている.
とする解法である.2次モデルでヘッセ行列を用いた場合(ニュートン法に対応する)やその近似行列を用いた場合(準ニュートン法に対応する)の信頼領域法の大域的収束性が示されている.
実際の応用では,目的関数値を単調に減少させることを緩和した非単調アルゴリズムや,ニュートン法において連立1次方程式を厳密には解かない非厳密ニュートン法などが効率的であることが知られている.また,大規模問題を解くためには,共役勾配法,ヘッセ行列のスパース構造を用いた信頼領域法,ベクトルの形でヘッセ行列の情報を更新する記憶制限準ニュートン法などが利用されている.なお,実際の数値計算では,導関数を解析的に与える代わりに,有限差分近似や自動微分を利用することも試みられている.
以上では微分可能な関数の最小化問題の数値解法を取り上げたが,実際には,目的関数が必ずしも滑らかであるとは限らない.こうした関数を最小化(もしくは最大化)する問題を微分不可能最適化 (nondifferentiable optimization) 問題といい,滑らかな関数を最小化する問題よりも解くのが難しくなる.目的関数 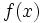 に凸性などの仮定をすれば,最適性条件は次式で与えられる.
に凸性などの仮定をすれば,最適性条件は次式で与えられる.
 は劣勾配の集合を表す は劣勾配の集合を表す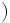 |
この条件を満たす点を見つけるためには,前述した数値解法がそのままでは使えないので,何らかの工夫をしなければならない.目的関数の劣勾配を利用したりヘッセ行列の代用品を利用することが考えられており,たとえば,バンドル法や一般化ニュートン法 (generalized Newton method) などがある[1, 2].
[1] J.-B. Hiriart-Urruty and C.Lemaréchal, Convex Analysis and Minimization Algorithms (I and II), Springer, 1993.
[2] 伊理正夫,今野浩,刀根薫監訳,『最適化ハンドブック』,朝倉書店, 1995.
[3] 今野浩,山下浩,『非線形計画法』, 日科技連, 1978.
[4] J.Nocedal and S.J.Wright, Numerical Optimization, Springer, 1999.
制約なし最適化と同じ種類の言葉
- 制約なし最適化のページへのリンク